(Mnova Lite 中不可用)
一维实验包含大量信息,但这些信息往往因信号重叠而模糊不清。同核耦合通常更容易通过扩展到二维来快速确定。使用两个频率维度则更容易确定异核耦合(例如 1H-13C)。二维实验使用一个频率维度和另一个轴上的其他变量(例如 DOSY 处理的 STE 实验,扩散系数在一个轴上),但本次参观将涉及两个频率(化学位移)维度。
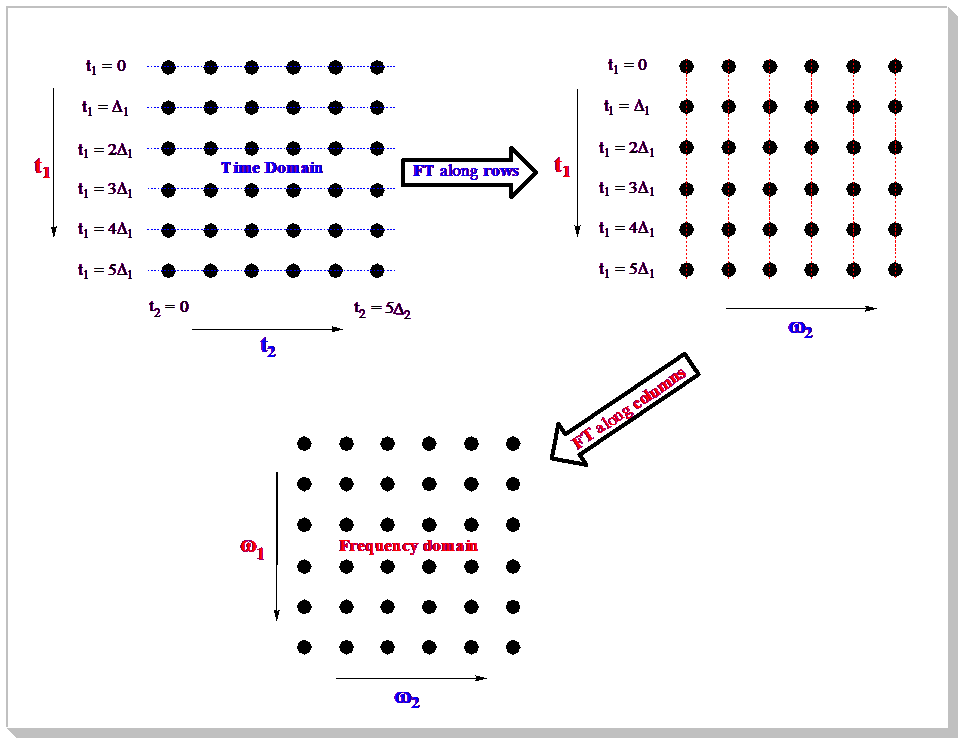
这些二维波谱是作为时域数据收集的,取决于两个时间变量(t1和t2),经过两次正交傅里叶变换后得到的频谱是两个频率变量的函数。 这些二维实验的一般方案如下脉冲序列所示:
在"准备时间",样品被一个或多个脉冲激发,自旋系统处于非平衡状态,随后将发生演变。在演化过程 中,所产生的磁化会自由演化。每个信号都将以其特征频率演化。然后是混合时间,其中包含一个或多个脉冲;正是在这段时间内,例如在间接检测过程中,磁化可能会从质子转移到 13C。 最后,信号被记录(检测)为第二个时间变量t2 的函数;然而,信号已被频率标记为t1 的函数。 在获取二维实验数据后,您将得到一个数据矩阵;行中包含在t1固定值和t2变化时收集的数据;它们实际上是正常的一维数据 FID。 列中包含在 t2的固定值和t1变化时收集的数据,它们是 "合成 "的一维 FID。该矩阵将进行两次傅立叶变换,一次是行变换,另一次是列变换。 这样,时间维度(t1和t2)就转换成了频率维度(f1和f2)。 在二维核磁共振实验中,我们可以在频谱的任一维度上找到任何核素,因此频谱可以显示相同核素(1H/1H)或不同核素(如1H/13 C、1H/15 N、1H/31P等......)之间的相关性。在二维核磁共振波谱中,采集维度(t2)是我们可以在不大幅增加采集时间的情况下获得更多数据点的维度。另一方面,在维度t1 中获取的每个点都会增加所需的扫描次数,从而大大增加总的采集时间。因此,在许多情况下,沿t1维采集的数据点数量要比沿t2 维采集的数据点数量少得多,但这一数据点数量必须始终足以提供足够的f1分辨率。 合成 "的f1FID 通常是截断的,可能会受益于前向线性预测。 使用 Mnova 处理二维 NMR 数据集几乎与处理一维 NMR 数据一样简单。您只需选择 FID 文件(或布鲁克公司的 SER 文件),二维谱图就会出现在您的屏幕上,无需触摸任何按钮。
在本教程中,我们将演示如何处理二维实验。本教程将指导您完成使用 Mnova 处理、显示和打印二维波谱的所有必要步骤。在尝试处理二维波谱之前,请阅读一维 NMR 处理教程, 因为您也需要能够处理一维波谱。
与一维 NMR 数据处理相比,多维(或二维)数据处理只需要几个新概念。一维 NMR 图谱可视为单个数据点矢量,将其转换到频域只需一个 FT。在二维波谱中,我们有一个二维点矩阵,需要对行和列进行傅里叶变换。
在二维同核和异核 NMR 中,点矩阵由一维 FID 阵列产生,由于其检测(以delta-t2 的间隔对 FID 采样)和t1的函数t2和t1的函数t1,因此每一个连续的 FID 的值都会递增,而t1的值决定了演化时间。第一行t1=0,第二行t1=Δ 1,第三行t1=2 Δ1,以此类推。同样的情况也会发生在数据列中,不过在这种情况下,样本间隔是不同的(Δ2)。
如上图所示,第一步是沿矩阵的行应用 FT,得到一个新的矩阵(干涉图),其中每一行对应t1的增大值,每一列对应一个运行频率变量 ω2。然后对各列进行工频处理,得到最终矩阵(二维频谱),其中频率轴(ω1)对应t1的变化,而ω2对应t2 的变化。
这种二维数据可以使用渐变函数进行处理,一旦获得二维频谱,就可以像一维处理那样进行相位或基线校正。 重要的一点是,处理操作需要在每个维度上进行。在 Mnova 中,处理总是沿采集维度开始,沿间接维度结束。
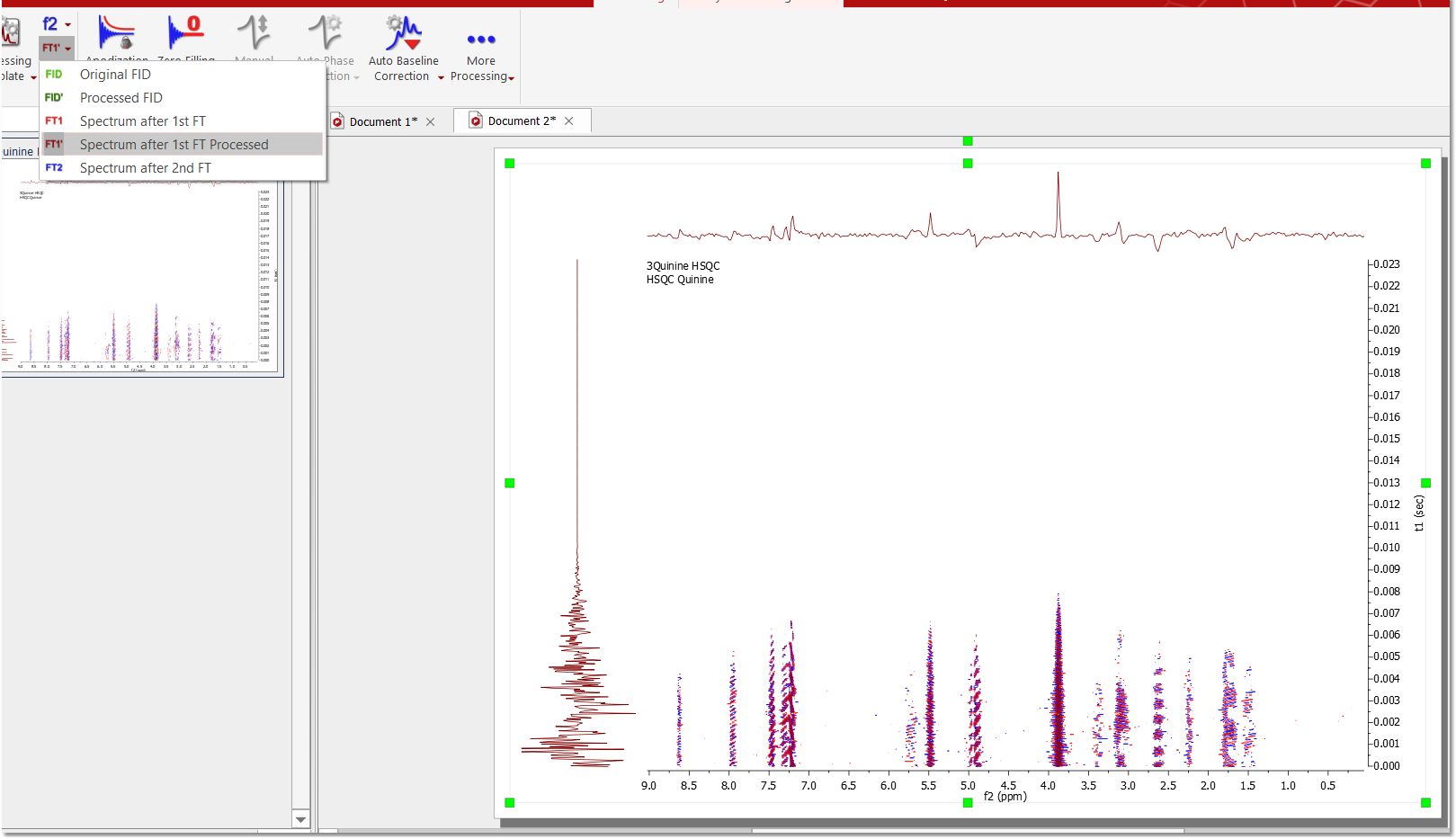
在本例中,我们将使用布鲁克波谱,因此您需要选择ser文件。选择后,您将立即获得处理后的频谱:
程序在运行过程中执行了以下一系列操作:
1.自动识别文件格式:程序将该文件识别为布鲁克文件,并使用相应的滤波器对数据进行解密 2.对于每个维度 -零填充 -傅立叶变换 -相位校正
用户可以在第一个直接维度的傅立叶变换之后,也可以在第二个傅立叶变换之前(在 t1 中)中断处理
基线校正
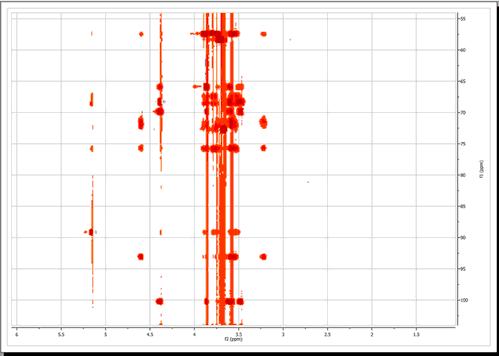
从上图中可以明显看到沿间接(f1)维度的基线伪影。通过基线校正 程序 可以轻松消除这些伪影 。点击 "基线校正 "图标 选择该选项
除非选中 "应用于所有尺寸 "选项,否则基线校正将应用于当前激活的尺寸。
您可以排除切割和盲区,或选择感兴趣的区域来应用基线修正。
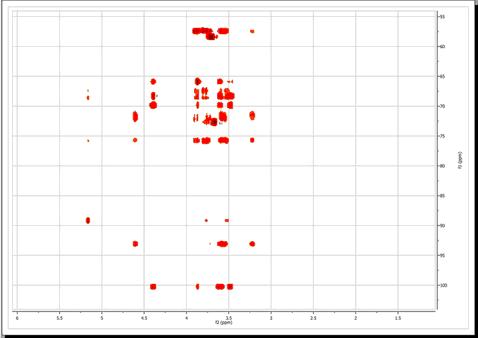
在当前情况下,由于当前处理维度为 f2,因此基线校正将仅沿该维度进行。这并不适合我们的情况,因为很明显基线失真主要出现在间接维度(f1)上。我们可以简单地将处理维度设置为f1,但更简单的方法是勾选基线校正对话框中的 "应用于所有维度 "选项。使用默认值进行校正后,得到的波谱就是这样:
用户只需点击"Show Traces(显示踪迹)"图标,即可显示 2D-NMR 图谱的踪迹
另请参阅 "在 2D-NMR 中显示迹线
关于实时频域处理的更多信息
在一维 NMR 处理 部分,我们介绍了实时频域处理概念。 同核二维实验的对角线抑制是这一概念的另一个例子。这种技术通常在混合时频域(干涉图)中进行。不过,在 Mnova 中您并不需要了解这一点。您可以在屏幕上显示变换频谱时抑制对角线。
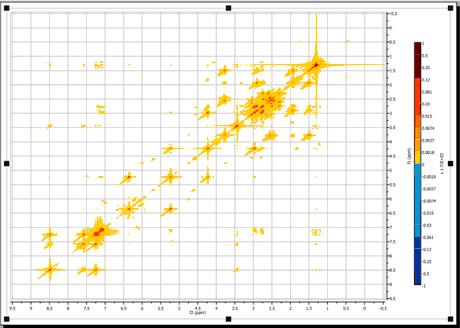
例如,下图显示的是二维幅值频谱:
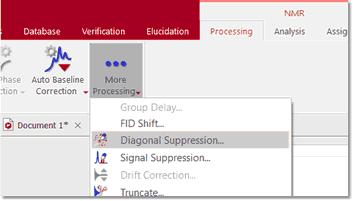
要抑制对角线,只需点击 FT 工具栏按钮右侧的小箭头(见下图),然后选择对角线抑制命令即可:
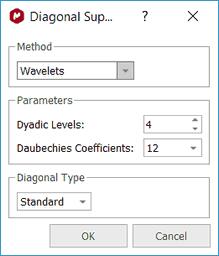
Mnova 为此提供了不同的算法。在本例中,我们将选择小波方法
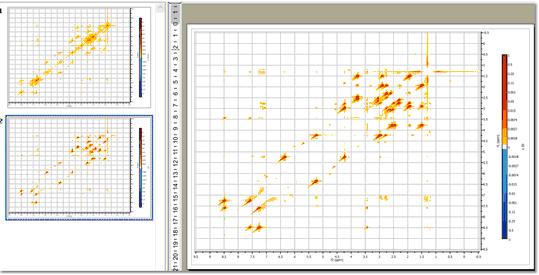
这就是生成的无对角线频谱。
请注意,上图中有两个页面,第一个页面包含带有原始对角线的二维频谱,第二个页面则是去除对角线后的频谱。
另请参见 |