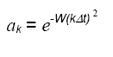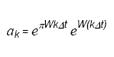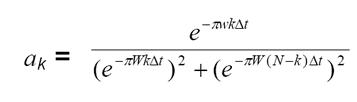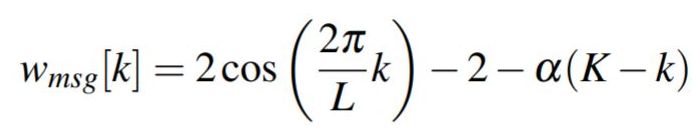Apodization (或 Weighting 或 Windowing):从字面上看,apodization 在希腊语原文中的意思是"切断脚" 。在这种情况下,"脚 "指的是信号快速衰减到零时出现的泄漏或晃动,会导致 FID 突然截断,例如在零填充时就会出现这种情况。在采集数据后,渐增是一种非常有用的方法,可以提高信噪比(灵敏度)或分辨率,甚至消除截断伪影。
最常用的微调函数是一条衰减的单指数曲线。衰减常数的大小决定了曲线衰减的速度。在普通的 FID 中,由样本引起的共振出现在信号的早期部分。将 FID 乘以衰减-指数函数时,就会偏向于时域的早期部分,并衰减采集期结束时的数据,而这些数据基本上都是噪声。单指数衰减函数在短时间内不会对信号产生明显影响,但会大大降低后期的噪声;而这是以增加线宽(即降低分辨率)为代价的。另一方面,如果使用指数递增曲线作为渐增函数,则会获得更细的线宽(分辨率提高),但会放大噪声(灵敏度降低)。
窗口功能是通过将数据矢量d 的元素逐个乘以矢量 a 来实现的。因此,矢量d的元素 k 乘以矢量a的元素 k,就得到了矢量d' 的元素 k。
d'k=akdk
难题在于如何找到一个矢量a,以减弱 FID 尾部的噪声,同时又不会造成过度的线宽;或者,在光栅化的情况下,如何使截断的数据以指数形式平滑为零,同时又不会造成过度的线宽。理论表明,当矢量a的衰减与矢量d 的衰减相匹配时,就能达到这一目的;在这种情况下,我们就得到了所谓的匹配滤波器。Mnova 允许在调整窗口函数衰减参数的同时观测最终波谱,从而使这一过程变得尤为简单。
Mnova 集成了多种窗口函数(指数函数、高斯函数、正弦钟函数、正弦钟方波函数、TRAF 函数、梯形函数、抛物线函数、汉宁函数、卷积差分函数和线性斜坡函数),这些函数可以组合使用,也可以交互使用(同时查看 FID 和生成的频谱),以提高灵敏度或分辨率。遗憾的是,很难找到同时提高灵敏度和分辨率的函数(特拉菲坎特函数可能是个例外,我们稍后会看到)。
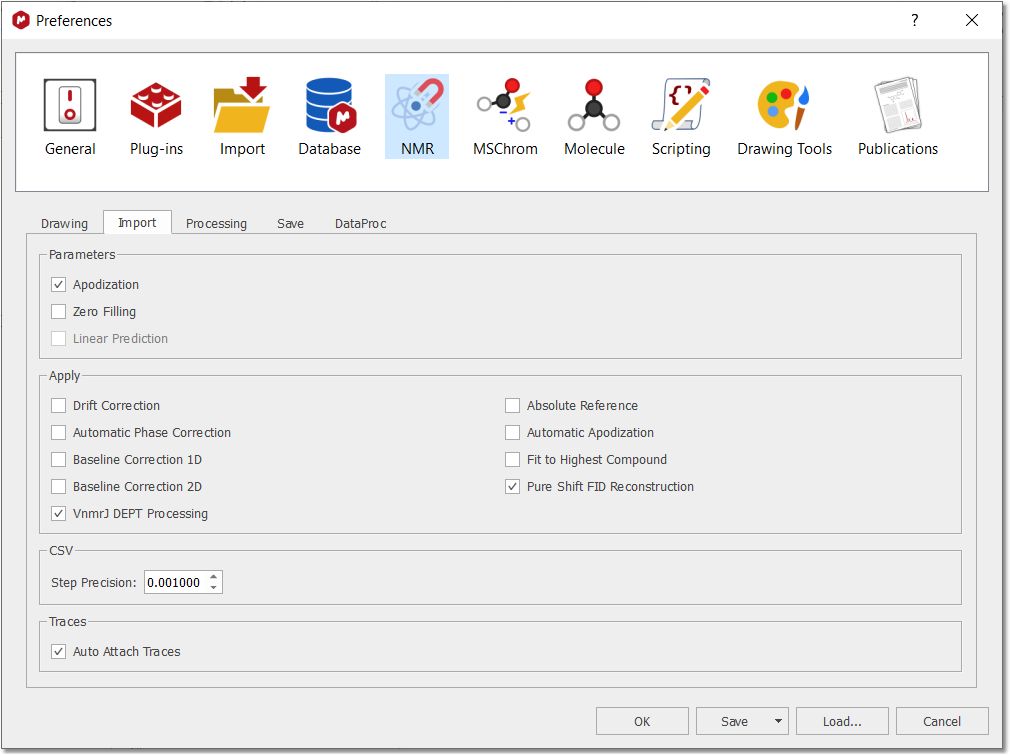
您可以通过菜单 "File/Preferences/NMR/Import"(文件/首选项/NMR/导入)导入波谱仪中使用的聚焦:
您也可以通过点击功能区的适用按钮,让 Mnova 应用建议处理。在这种情况下,Mnova 将在 1D 中应用4.0 的 Stanning 精确度(对于 13C,它将添加 2.0 Hz 的指数精确度)。对于 2D,它将应用 2.0 Hz 的指数渐增和 Stanning 4.0(如果是 F2),并在 F1 中应用 Sine Square 90º(第一点:0.5)。
可以在 "处理 "功能区(快捷键:W)中找到渐增功能:
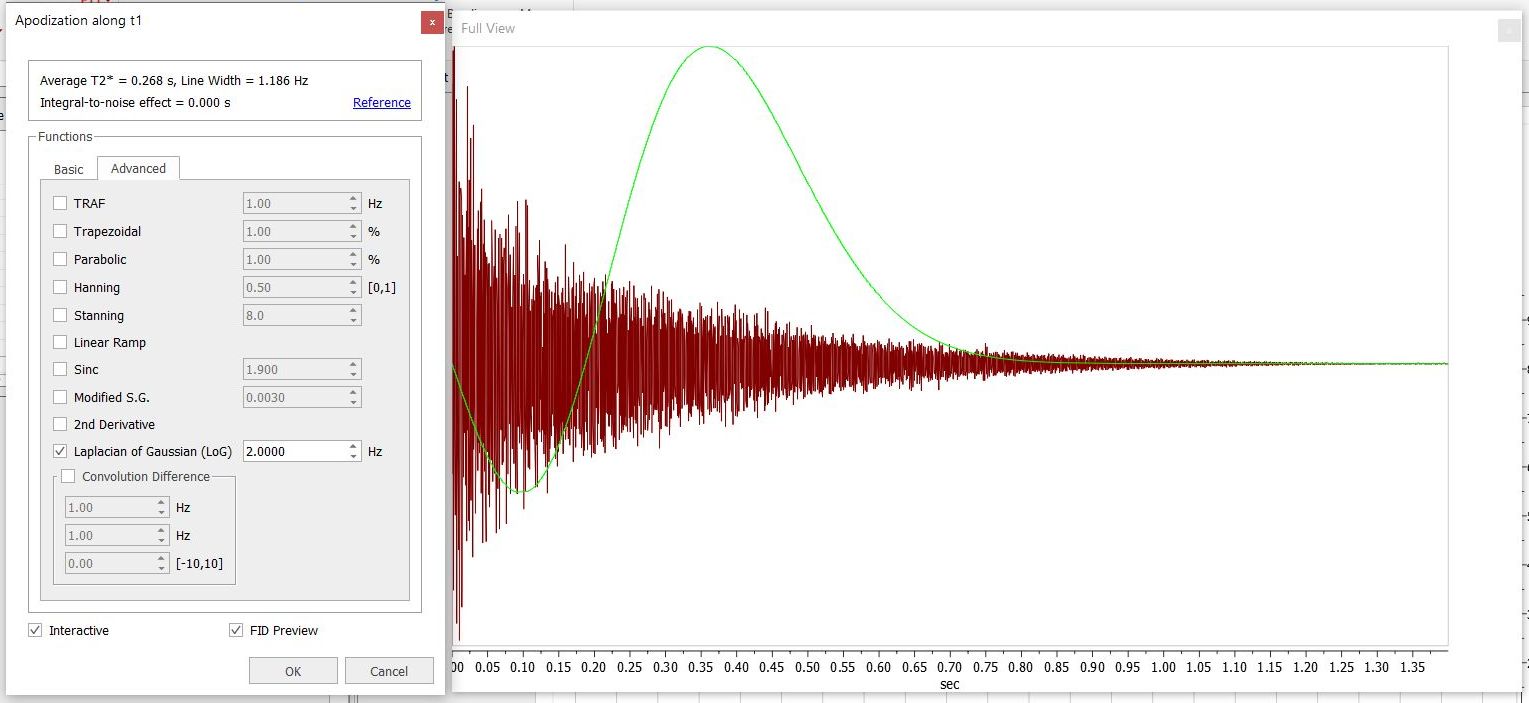
选择"Apodization "后,将显示一个无模式对话框:
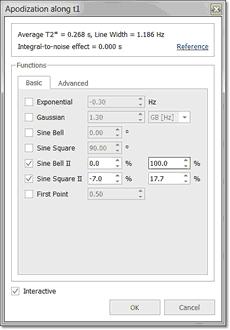
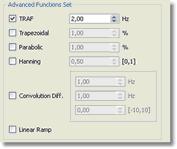
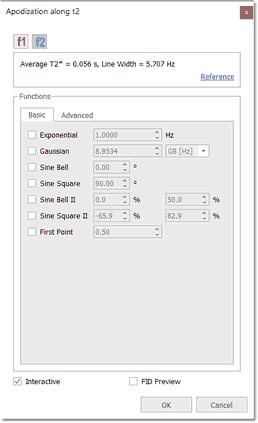
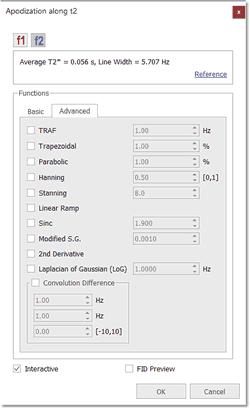
由于这是一个无模式对话框,您可以 在对话框打开时更改波谱的强度。 在 2D-NMR 波谱中,您可以从 F1 切换到 F2 以选择所需的光栅化功能。 在此对话框中,您可以找到 Mnova 在 FT 之前应用的窗口函数类型,以及其他标准函数(高斯、正弦钟、正弦平方和第一点)。如果选择 "Advanced(高级)"选项卡,您还可以设置其他光栅化函数,如下所示:
为了帮助用户找到最合适的窗口函数及其参数,Mnova 允许用户交互式调整窗口函数的参 数,并直接查看对频谱的影响。为此,请确保勾选了 "交互式 "复选框,然后您就可以通过使用以下按钮跟踪所应用的函数在频 域频谱上(或在 FID 上,如果您在 "FID "视图上)产生的确切效果
我们将尝试简单明了地解释这些功能的应用和效果:
指数: 指数渐增函数的定义如下
ak = e-πWkΔt 其中W (需要调整的参数)表示以赫兹为单位的线宽因子。因此,如果信号的原始宽度为 "L",则应用此窗函数后信号的最终宽度为"L+ W"。如果W为正值,我们就会得到一条指数衰减曲线 (我们会给 FID 开始处的点更多权重,而抑制时间序列末尾的数据,这些数据基本上都是噪音)。正如我们之前所解释的,这将提高频谱的"灵敏度"(信噪比),但代价是线宽的增加(分辨率的降低)。
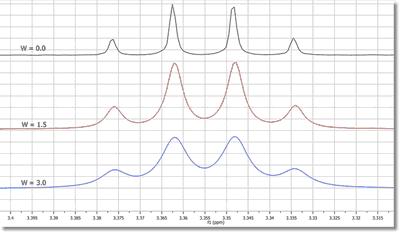
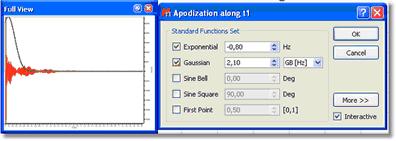
下图显示了W 对线宽的影响。黑色轨迹没有应用窗口函数。红色轨迹显示,由于应用了指数函数,信号增大,信噪比(匹配滤波器)提高;而蓝色轨迹显示,如果指数函数过于严重,线宽会再次减小信号的大小。
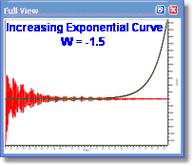
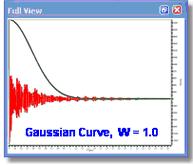
如果W为负值,我们就会看到指数曲线不断上升,从而得到相反的效果(分辨率提高,线条更细,灵敏度降低,即信噪比降低)。下图显示了在 FID 上指数曲线递增和递减的 区别(在 "全视图 "窗口中显示)。请注意,在这种情况下,指数递增曲线并不是一个好的选择(它通常与高斯等其他函数结合使用)。
在大多数文献中,该参数用 LB(线展宽)表示。
高斯: 高斯窗口函数类似于统计分析中使用的高斯概率分布函数。高斯函数以准指数方式上升到其单个最大值,然后以同样的方式回落到零,因此几乎可以看作是两个背靠背的指数。
在高斯倍频法中,FID 的每个数据点都乘以矢量:
其中 W与指数极化中使用的加宽因子相同。该函数与指数函数类似,但在 FID 开始时衰减相对较慢,而在 FID 结束时衰减相当快。因此,与指数倍增法相比,它引起的线展宽较小。
在下一张图片中,您可以看到W对线宽的影响:
高斯加指数: 该函数也被称为洛伦兹到高斯变换(Lorentz-to-Gauss Transformation),在 Mnova 中并未直接实现,但您可以通过勾选指数和高斯乘法函数,并为指数线展宽(W)引入负值,为高斯参数(GB)引入正值来应用该函数。通过适当调整这些参数,可以优化波谱的分辨率。
因此,该加权函数结合了上升的指数函数和下降的高斯函数;那么,得到的矢量将是 要使用 Mnova 执行指数/高斯加权,请在工具栏上的 FT 滚动菜单中选择加权选项,然后点击 指数和高斯分辨率增强选项,最后输入 W(或 LB)和 GB 的适当值并点击确定。 通常情况下,需要通过反复试验来调整参数,直到获得最佳效果。您可以(通过勾选 "交互式 "方框)在频域频谱或 FID 窗口(在 "全视图 "窗口中以图形显示)上跟踪所应用函数的确切效果,如下截图所示。
GF(高斯系数)是一个介于 0 和 1 之间的数字,它定义了函数的最大值,即采集时间的一部分。
正弦钟 (Mnova Lite 中不可用): 在 NMR 实验中,如果感兴趣的信号在 FID 开始时不是最大值,那么该功能就非常有用;对于幅值波谱,该功能也非常方便,因为它可以减少线形的色散部分。 在 COSY 实验中,交叉峰是正弦调制的,而对角线峰是余弦调制的。因此,正弦钟窗口法可以突出十字峰,削弱对角线信号。遗憾的是,由于某些信号的弛豫时间不同,可能并不是所有的交叉峰都会在同一时间达到最大值;在这种情况下,可以对正弦波钟进行移位,以获得最佳的折衷波谱。未移位的正弦曲线还可以从绝对值 COSY 中去除色散信号,从而提供所需的吸收线形状。
避免将此函数用于一维波谱,因为它会降低波谱强度。如果与相位敏感实验一起使用,正弦钟会导致信号出现负侧裂和积分接近零。
该函数包括将 FID 的每个数据点与下一个向量相乘:
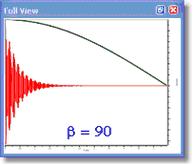
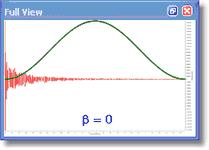
Mnova 要求输入以度为单位的β 参数。当β = 0 时,等效函数为正弦波;当β = 90 时,等效函数为余弦波。在下面的图片中,您可以看到不同的β 值所产生的正弦钟形函数的表示方法:
在二维-HSQC 实验中,正余弦钟远地点化(β = 90) 非常方便:
您可以使用 "类似于 VNMR 版本的正弦加权",它使用的是采集时间的百分比(而不是秒),以便使参数适用于已保存处理模板的其他波谱。
位移正弦 II 的完整公式为 sin(((t-sbs)*pi)/(2*sb))。
其中,sbs = sbs Mnova /100*T AQ;sb = sb Mnova/100*T AQ
对于小于零的函数值,函数将被截断(即只使用第一组正值)。
正如您所看到的,您还可以调整正弦波的时间周期(就像 VNMR 中的 "sb "参数一样)
正弦方波 (不适用于 Mnova Lite): 正弦钟加权函数的形状通过平方来改变,从而产生正弦钟平方函数,它更集中于最大值。使用 90° 移位的正弦钟平方对二维相位敏感实验进行光栅化非常有用。
第一点校正: 离散FT 与连续FT 之间有一个重要区别。离散FT 会产生基线的恒定垂直位移,这可能是由于 FID 的第一点失真造成的。它将 FID 视为一个周期性重复的函数,因此 t=0 时的纵坐标将代表第一个点和最后一个点的代数平均值。在大多数 FID 中,最后一点的值非常接近于零,因此第一个实数点必须先除以 2 才能引入 FT 算法。通常有必要在 FT 之前将 FID 的第一个点乘以 0.5,以确保频谱上的积分值等于 FID 第一个点的值。
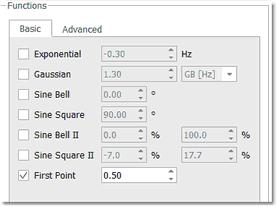
您可以通过输入所需的值来更改该乘法参数(默认值应为 0.5,如下图 FT 对话框所示)。
以下功能可通过 "Apodization(渐变)"对话框中的 "More >>(更多 >>)"按钮访问。
Traficante (不适用于 Mnova Lite): 指数乘法高斯以及两者的组合可以提高波谱分辨率,但会损失一定的信噪比。Traficante 窗口功能可在不明显降低信噪比的情况下提高分辨率。特拉菲坎特增强了 FID 的中间部分,然后使用匹配滤波器衰减时间序列后半部分的噪声。这一过程包括用 FID 的平方和除以 FID 的反向平方和。如果有 N 个数据点,则原始 FID 中的第k 个点为 k 点,而反向 FID 中的适用点为 (N-k) 点。由于得到的 FID 是对称的(相对于中点),我们可以将其乘以一个函数,从而得到一个新的不递减的理想 FID。
因此,如果我们将原来的 FID 命名为E,将反转的 FID 命名为 ε,我们将得到
E-g(t)+ε-h(t) = 1
特拉菲坎特光栅化就是将 FID 与下面的矢量相乘:
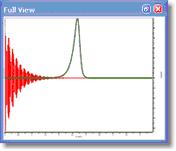
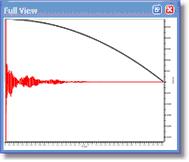
在下图中,我们可以看到特拉菲坎特函数(W= 2)应用于 FID
梯形 (Mnova Lite 中不可用): 此函数 将 FID 乘以梯形函数;
其中 T 是采集时间,k是数据总长度的百分比。
该选项有助于避免因截断 FID 而产生的 "sinc "假象。您可以在 FT 菜单的高级功能中选择数据总长度在 0% 和 100% 之间的百分比(k)。
抛物线 (Mnova Lite 中不可用): 此功能 将 FID 乘以抛物线形状的函数,其中
您还可以设置抛物线的长度,方法是选择(FT 滚动菜单上的)Apodization,点击 "更多", 选择抛物线,然后选择所需的参数值(b,用数据总长度表示)。同样,通过(预)选择 "全视图 "窗口,您可以看到应用的函数对频域频谱的确切影响或对 FID 的影响:
汉宁 (Mnova Lite 中不可用): Mnova 采用以下通用方程:
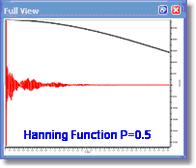
您可以在 FT 对话框的高级功能设置中设置该参数。如果P = 0.5 ,我们将使用汉宁函数;如果 P= 0.54 ,我们将使用汉宁函数,分别产生 10%和 20%的线展宽。汉宁窗(更正确的叫法是汉恩窗和汉明窗)属于 "高次余弦 "函数系列,也包括高斯窗。这些函数与余弦钟一样,都有一个最大值;Mnova 通常在零时实现这些函数的最大值。汉宁函数有时用于减少混叠。当信号采样不足(违反奈奎斯特准则),导致频谱折叠时,就会出现混叠现象。这会导致峰值出现在不正确的位置,而且通常不会与真实信号同步。出现这种情况的原因是实验设置不正确(信号超出了频谱宽度的高频端),而在采集后对其进行校正的能力确实非常有用。
卷积差分 (Mnova Lite 中不可用): 该加权函数将 FID 乘以 :
其中LB为线展宽,SW为波谱宽度(以赫兹为单位)。您也可以通过 FT 图标的滚动菜单访问此功能,设置 LB 值。
线性斜坡 (Mnova Lite 中不可用): 该命令用于将 FID 的数据点乘以递增的线性斜坡,从而得到傅立叶变换频谱的一阶导数 { d(强度)/d(频率)}。 这将以牺牲信噪比为代价,突出频谱中上升较快的部分。如果初始频谱具有极佳的信噪比,该功能可显著提高分辨率。 Mnova 将很快提供使用小波处理的衍生物,它能产生更好的波谱。
这种加权函数会给 FID 末端更大的权重,从而放大噪声(降低灵敏度),因此我们建议仅将其与另一种给 FID 开始更大权重(提高灵敏度)的函数结合使用。在实际应用中,可以将斜坡函数添加到已经用 EM 函数(一维)或正弦-钟形函数(二维)进行窗口化的频谱中,以提高选择性。
修正的萨维茨基-戈莱(时域)由于萨维茨基-戈莱窗口在信号开始时为零,我们建议在其上添加一个递减斜坡。这就是修改后的萨维茨基-戈莱窗口:
其中,α 是斜坡的权重。α 越大,原始信号的权重就越大,信噪比增益就越高,但分辨率却会降低。
二阶导数: 作为现有一阶导数 的扩展(多年前已经实现,包括线性斜坡的应用)。
高斯的拉普拉斯函数 二阶导数窗口的形式为w2[n] =k2
|


 .
.