Fourier Transform

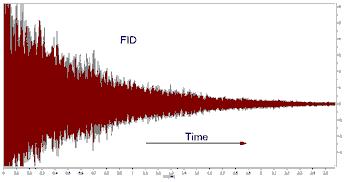
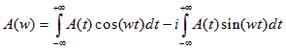关于 FT 的基本概念

现代NMR采用脉冲射频能量一次性激发所有频率。脉冲发出后，信号会立即以时域干涉图的形式被检测到，时域干涉图包含了样品在不同核共振频率下发出的所有阻尼正弦波信号的总和。

信号会随着时间的推移而衰减，因为各种弛豫机制会使 X-Y 平面上的磁化去相或使磁化返回 Z 轴。由此产生的干涉图称为 自由感应衰减 （FID，见下图）

如果您仔细观察上图中的 FID，就会发现它是由多个频率组成的。此外，如果您能够在给定的时间段内（例如 1 秒）计算峰值和谷值的数量，那么您就可以测量周期并计算出组成 FID 的某些信号的频率。

在 "现实 "生活中，您并不需要手工进行这种转换。幸运的是，让-巴蒂斯特-约瑟夫-傅里叶（Jean-Baptiste Joseph Fourier）在研究热流时提出，变量的任何函数都可以用该变量的正弦谐波倍数之和来表示。这项工作后来发展成为傅里叶级数。

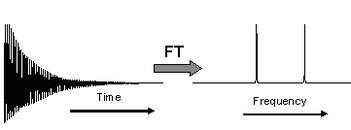
傅里叶的提议部分导致了线性映射算子的发展，该算子可将给定函数映射到其他函数，在我们的特定情况下，将时间函数映射到频率函数。 为了纪念傅里叶，这个算子被命名为傅里叶变换。简而言之（数学细节不在本文讨论范围之内），傅里叶变换或 FT 是将时域函数（FID）转换为频域函数（频谱）的数学过程，如下图所示：

因此，FT 是一种从 FID 生成频谱的数学过程。它通过 FID 搜索频率信息，并生成信号强度与频率的关系图。如果频率信息定义明确，峰值就会很尖锐，但如果信息不精确，峰值就会更宽。

连续傅立叶变换的细节包括以下等式：

其中，A(w)是信号强度与频率的函数关系，A(t)是 FID 信号强度与时间的函数关系，i 是 (-1)/1/2。

将实部和虚部分开，我们可以得出

实部可视为与接收机参考振荡器同相的信号分量，而虚部则是与接收机参考振荡器反相 90 度的信号分量。

原始傅里叶变换是为连续变量的函数定义的： 为了满足脉冲 NMR 的需要，即在短时间内对 FID 进行采样，使用所谓的离散傅里叶变换(DFT)。当使用离散时间间隔采样测量信号强度时，傅里叶积分将被以下值取代：

其中，N是采样点数，n 是 第 n 个采样点，2πk 是乘法器，用于将n 点转换为与wt（单位：rad/s）相对应的值。如果我们有一个由N 个信号点组成的随时间变化的函数集合（命名为A），那么计算适用的实频点和虚频点阵列就非常简单，可以通过计算机轻松完成。

多点计算显然会很慢（尽管目前的计算机计算速度极快），但点越多，曲线图就越平滑。为了缩短计算时间，我们可以使用库利-图基快速傅里叶算法（FFT），将DFT的计算次数从N*N减少到FFT 的Nlog2N。 如果N为 1024 个采样点，计算时间将从1048576 减少到 7098，即减少 93%。 该算法有一个特殊限制，即N必须是 2 的幂次（在点数不是 2 的幂次的情况下，Mnova 将通过向下一个更高的 2 的幂次添加零来扩展 FID 的大小）。

库利-图基FFT算法之所以能惊人地缩短计算时间，部分原因在于它采用了一种称为 "位反转 "的方法，避免了内部矢量分量计算的重复。该算法还通过识别某些计算的正交性来节省时间，只需改变一个代数符号，或颠倒正弦和余弦项，就能从一个向量计算出另一个向量。这一过程是分而治之算法一般技术的一个例子，在许多传统算法中都很明显，即把一个工件分割成其他更多更小的工件。

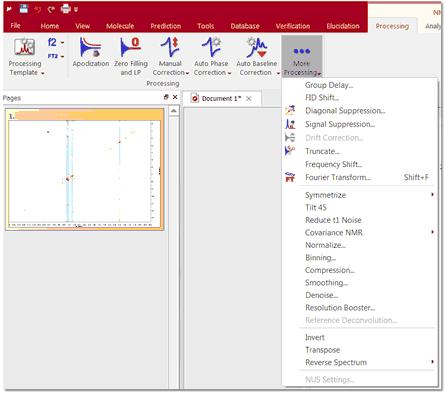
尽管如一维和二维 NMR 处理项目所述，Mnova 默认在傅立叶变换和傅立叶变换之前应用所有处理参数，但该软件还包含大量用户可应用的算法，以尝试优化所获结果。因此，在 "更多处理 "图标的滚动菜单中，用户可以找到以下应用选项：

FT 的快捷键是 "Shift+F"。

FT 和 Mnova

初看起来，普通的 FFT 就足以获得所需的频谱。但在很多情况下并非如此。虽然 Mnova 会通过零填充调整采样数以获得 2 的幂次，但用户可以选择进一步增加零填充，将获取的 2 的幂次值增加一倍，以获得最佳的 "频率 "分辨率，甚至进一步提高 "数字 "分辨率。

与 FFT 算法密切相关的其他操作包括

-正交检测

-漂移校正

-数字滤波

-相位敏感协议