Smoothing

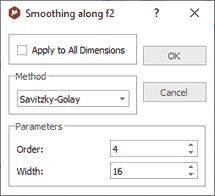
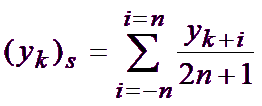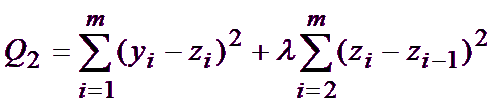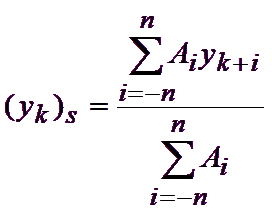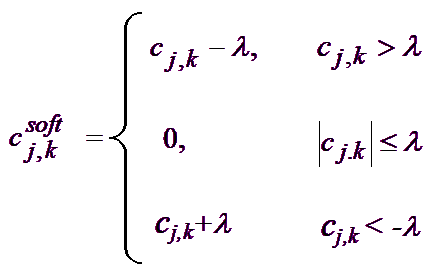平滑 （Mnova Lite 中不提供）：

频谱的信噪比（S/N）可通过平滑（或滤波）技术来增强。该技术用于减少噪声对频谱的影响，并有可能揭示蕴含在噪声中或被噪声扭曲的信号。噪声包含快速波动，其速度通常快于真正信号的变化速度。平滑法对频谱数据进行低通滤波器处理，以去除这些快速波动，同时将对信号的影响降至最低。

Mnova 融合了一些常用的信号平滑算法。

通过菜单 "处理/更多处理/平滑 "可使用该命令。随后将打开一个对话框：

用户可以在方法滚动条中选择平滑算法（移动平均滤波器、惠特克平滑器、萨维茨基-戈莱或小波）。用户还可以将平滑应用于所有维度（通过勾选适用的复选框）。

移动平均算法"：用于平滑等距点信号的较简单软件技术是移动平均法。原始（噪声）数据数组（y1、y2、...、yN）可转换为新的平滑数据数组。平滑点"(yk)s 是原始数据 yk-n、yk-n+1、...、yk-1、yk、yk+1、...、yk+n-1、yk+n 的连续 2n+1（n = 1、2、3、...）个奇数点的平均值，即

奇数 2n+1 通常称为滤波宽度（或 Mnova 中的跨度）。滤波宽度越大，平滑效果越强。

当滤波器通过的峰值比滤波器宽度窄时，移动平均算法的破坏性就特别大。

用户可以在对话框中选择所需的滤波宽度（跨度）。

惠特克平滑器 Whittaker 在 1923 年提出了一种平滑算法。如果y是 m 个数据点的序列，z是应近似y 的平滑序列，则我们将其最小化：

第一项衡量 z 与 y 的拟合程度， 第二项是所谓的惩罚：它抑制 z 的变化。惩罚的影响可通过 参数λ 来调整；选择的λ 越大， z 就越平滑，但代价是数据拟合度越差。

用户可以在对话框中选择平滑系数，也可以让 Mnova 自动检测最佳平滑系数。

萨维茨基-戈莱算法"： 比简单求平均值更好的方法是对一小部分连续数据点进行最小二乘拟合，并将拟合后的多项式曲线的中心点作为新的平滑数据点。

萨维茨基和戈莱指出，可以得出一组整数（A-n、A-(n-1)......、An-1、An），并将其用作加权系数来执行平滑操作。使用这些加权系数（称为卷积整数），结果完全等同于用多项式拟合数据，如前所述，而且在计算上更有效，速度更快。因此，萨维茨基-戈莱算法的平滑数据点 (yk)s 由下式给出：

用卷积整数集代替平滑后的信号，可以直接得到其 1 阶、2 阶......、m 阶导数，因此萨维茨基-戈莱算法非常适用于计算由离散点和等距点组成的噪声信号的导数。

萨维茨基-戈莱算法的平滑效果不像移动平均法那样强烈，对重要信息的损失和/或失真相对有限。不过，需要强调的是，这两种算法都是 "有损 "的，即部分原始信息会丢失或失真。这种平滑处理只具有表面价值。

用户可以选择 "阶次 "和 "宽度"。

小波 小波阈值处理是基于小波的降噪技术的基础。对于具有 高斯噪声的函数f

这意味着函数f 将被 还原。

硬阈值是一种简单的 "保留或删除 "选择。所有低于阈值λ的小波系数都被清零。

软阈值则将系数缩小为零：

现在最重要的一步是正确选择阈值λ。

通用阈值 包括

其中n 是 样本大小，σ 是标准偏差尺度上的噪声尺度。

噪声抑制的整个过程包括小波变换 (WT)，产生小波系数cj;k， 然后对这些系数进行阈值处理，最后进行反小波变换 (IWT)，恢复原始频谱。

用户可以选择比例（σ）和分数阈值（λ%），也可以选择软阈值或通用阈值（勾选适用的方框）。