主成分分析(PCA)是一种使用正交变换将一组相关变量观测值转换为一组线性不相关变量值(名为主成分)的程序。
如果您拥有化学计量学插件的许可证,就可以使用 Mnova 进行 PCA 研究。
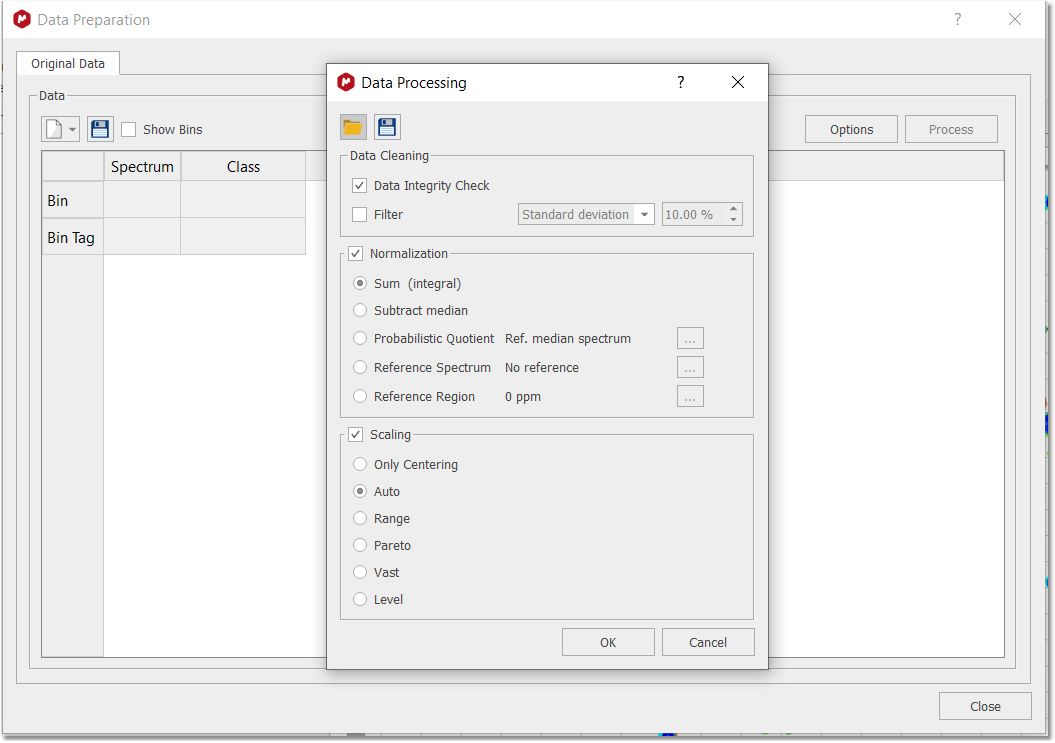
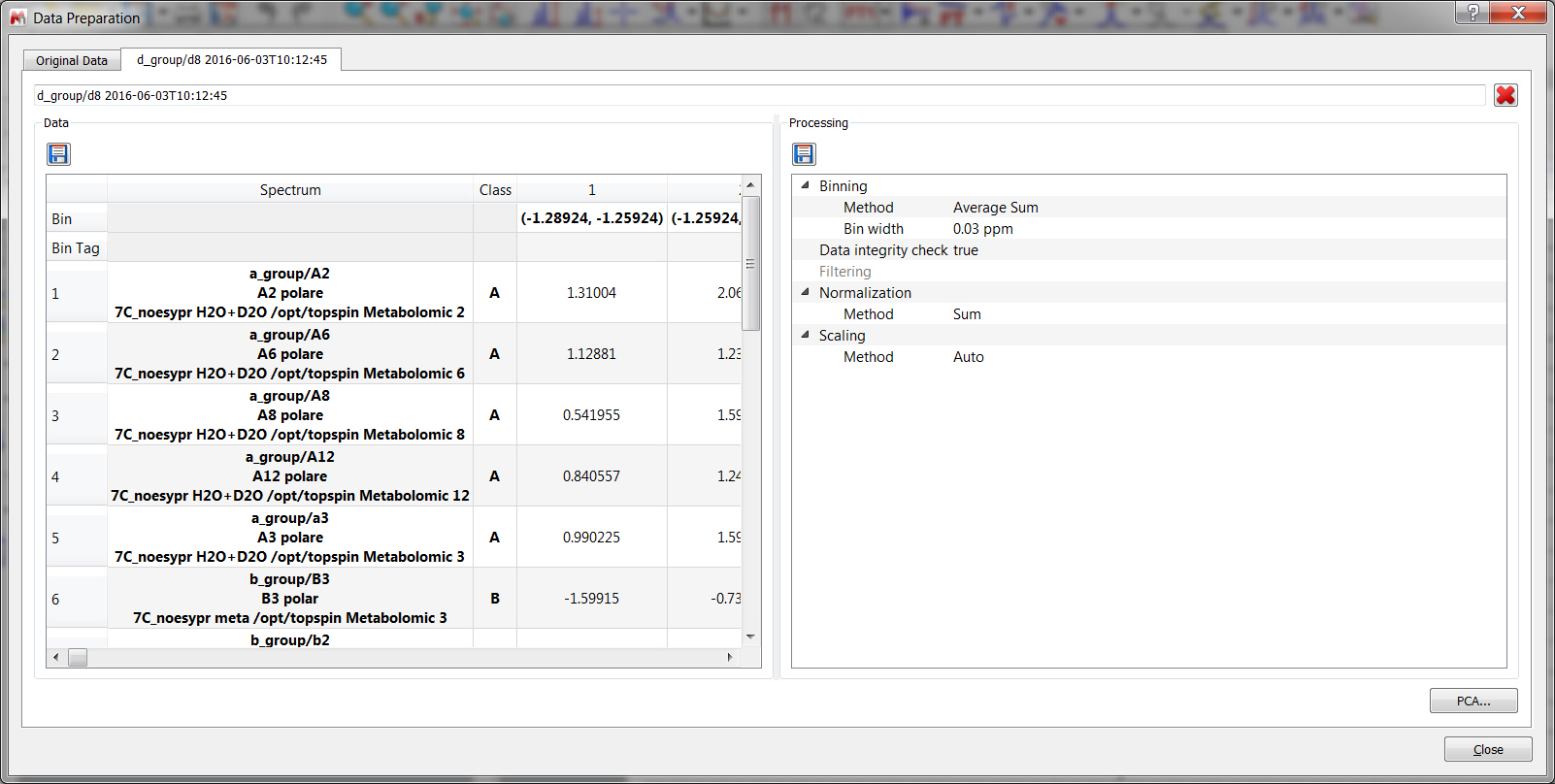
您只需加载一维或二维堆叠波谱,然后点击菜单 "化学计量学/数据准备"。点击选项按钮将显示 "数据准备 "对话框:
数据清理:有两个选项可同时使用。 a.数据完整性检查(Data Integrity Check):将负值(负积分)替换为零。 b.过滤。过滤方法用于删除空仓和不显示波谱序列间任何变化的仓。默认情况下,如果一个变量(分仓)在所有行(波谱)中显示为零,则该变量(分仓)将被剔除。可以有五个选项。在前三个选项 "标准偏差"、"中位数平均值 "和 "IQR "中,将丢弃固定比例(默认为 10%)的分位数(例如,如果矩阵由 100 个分位组成,则意味着丢弃 10 个分位,选择基于所选的过滤方法)。实际上,标准偏差、绝对偏差中位数和四分位距都是针对所有分仓计算的。此外,还将放弃一定数量的分区(具有最低 SD 值、中位数绝对偏差或 IQR 值),具体数量按分区总数的百分比计算。 在计算平均值或中位值时,用户需要输入平均值或中位值。这样,只有显示值低于输入值的数据箱才会被丢弃。 归一化:这是对矩阵行进行的操作。可以选择四种可能的策略: c.求和:将某一行的每个元素除以同一行所有元素的总和; d.减去中值:将一行中的每个元素减去构成同一行的所有分区的中值; e.Probabilistic Quotient(概率商): Hans Senn 等人提出的归一化方法。更多信息,请查阅本文:Anal.Chem.2006, 78, 4281-4290 f.Reference Spectrum(参考波谱或参考波谱系列):通过和进行归一化处理后,一行中的每个 元素都将被所选参考波谱行中的相应元素除以(例如,当您有一个参考波谱并希望将其 与所有其他波谱进行比较时)。如果您选择了一束波谱(如属于同一类别的所有波谱),则会对计算出的平均波谱进行归一化处理。 g.参考区域(或分区):用户输入感兴趣的参考峰的化学位移值或范围(ppm),MNova 会自动识别包含所选峰/区域的分区。此外,一行中的每个分量都会被相应行的参考分量除以。 缩放: 这是对矩阵列进行的操作。有五种不同的方法可供选择:自动缩放、范围缩放、帕累托缩放、巨大缩放和水平缩放。应用的数学运算如下:
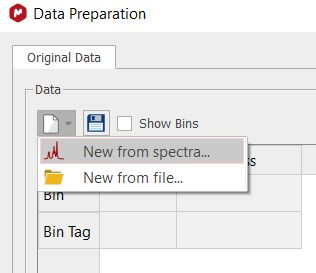
有关不同缩放方法的更多信息,请访问此 链接。 下一步是选择 "从频谱新建"(如果有其他实验保存的 "制备文件",则选择 "从文件新建"):
选中 "Show bins(显示分段)"复选框,在堆叠图中显示分段。
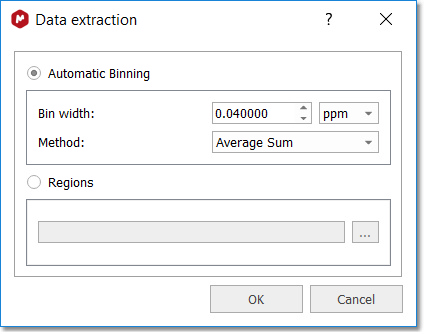
将出现一个新的对话框来选择分选 选项:
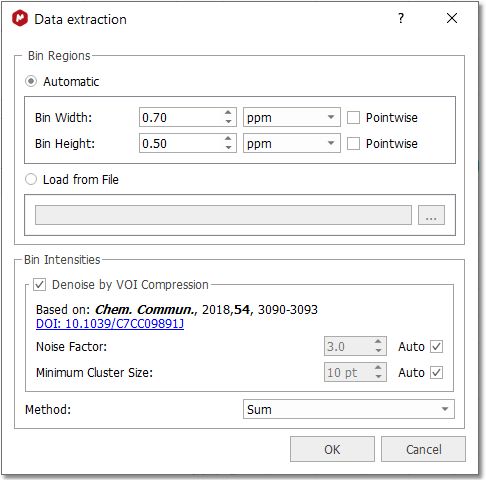
如果使用的是二维堆叠数据集,则会出现此对话框:
您可以自动或通过加载文本文件计算分选区域: -自动:使用固定的二进制大小创建二进制区域。您可以将 bin 宽度或 bin 高度设置为Pointwise,以便在该维度上使用频谱分辨率。 -从文件载入:从任何现有的 "MestReNova 积分区域文件"(可从任何集成波谱中获取, 并点击菜单 "文件/保存为/MestReNova 积分区域 (*.txt)")中导入 bin 区域。
在这里,您可以执行 VOI(Variable Of Interest,兴趣变量)压缩,以减少感兴趣的分区数量。建议对分选方法进行压缩:求和、平均求和和居中。
有四种分选方法可供选择:和值、平均和值、中心和峰值。Sum "方法将对一个分隔桶中的所有点求和,"Average Sum "方法将用和除以分隔桶中的点数,而 "Center "方法将只返回分隔桶中间的值。例如,如果一个数据桶有 5 个点,它将返回第 3 个点的值。峰值 "方法将首先执行 GSD(全局波谱解卷积),然后对峰值表进行分选。对于大型数据集(超过 50 个堆叠波谱,建议在执行 PCA 模块之前先执行 GSD)。 点击 "Process(处理)"按钮后,会弹出一个新的对话框,对处理过程进行总结,并允许您保存 "Data preparation file(数据准备文件)"或 "Processing(处理)"文件,以便将来使用:
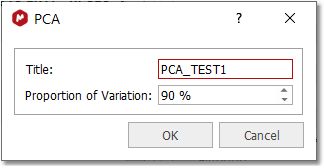
最后,点击 "PCA 按钮 "选择变异比例(主成分数)并更改标题:
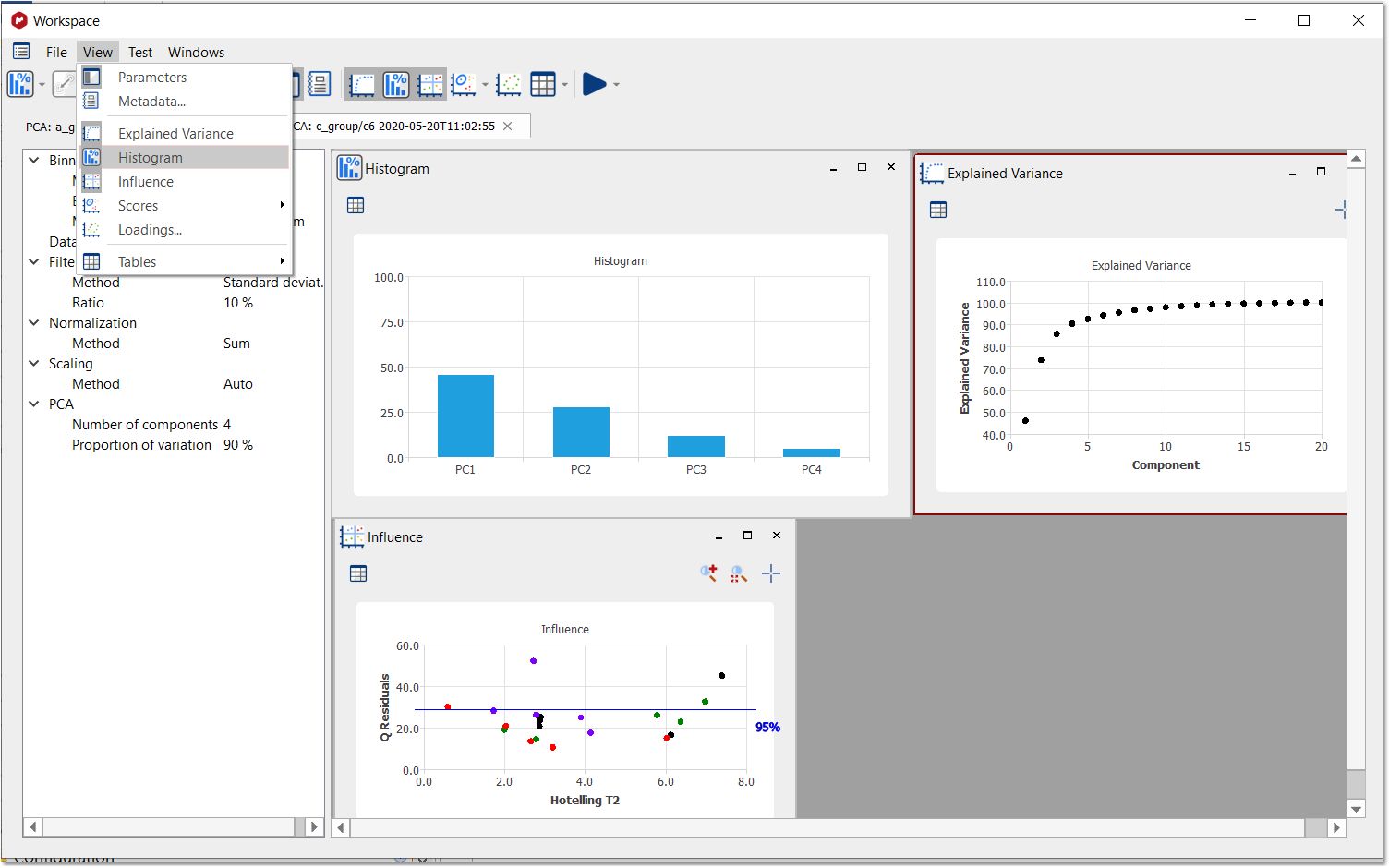
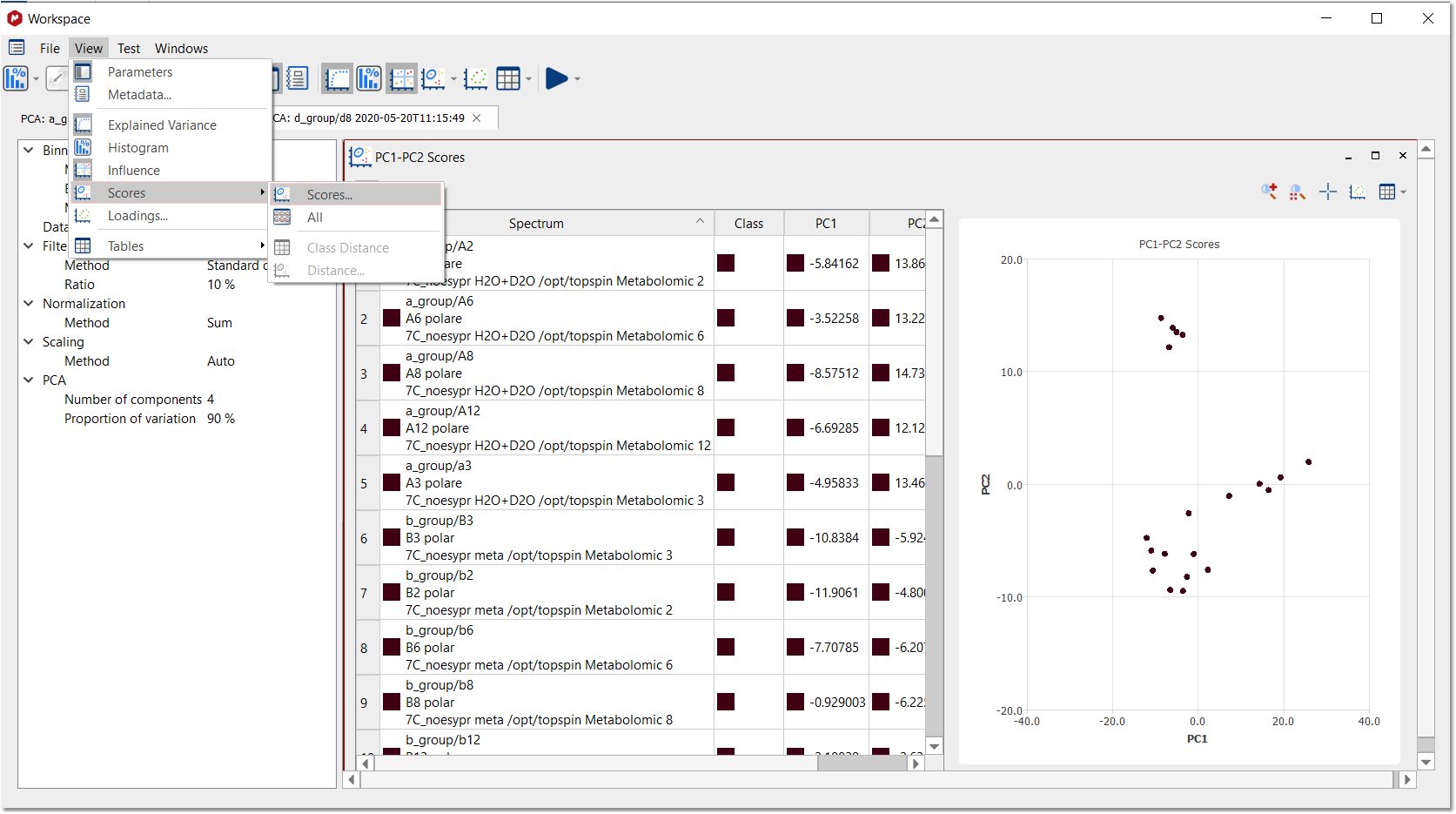
点击 "OK(确定)"按钮后,将显示 "工作区面板"。在 "视图 "菜单中,可以显示 "解释方差"、"直方图 "和 "影响 "图表。右键单击(或 Ctrl/Cmd+C)任一图形,可以复制到剪贴板、报告或保存图像:
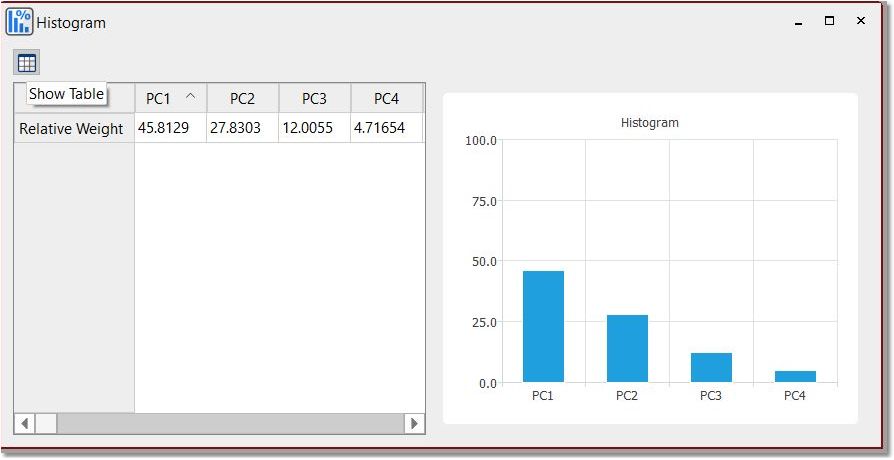
点击 "显示表格 "按钮,将隐藏/显示包含各成分相对权重的适用表格:
从 "查看/分数 "菜单中选择 "分数图 "选项卡,将显示如下窗口:
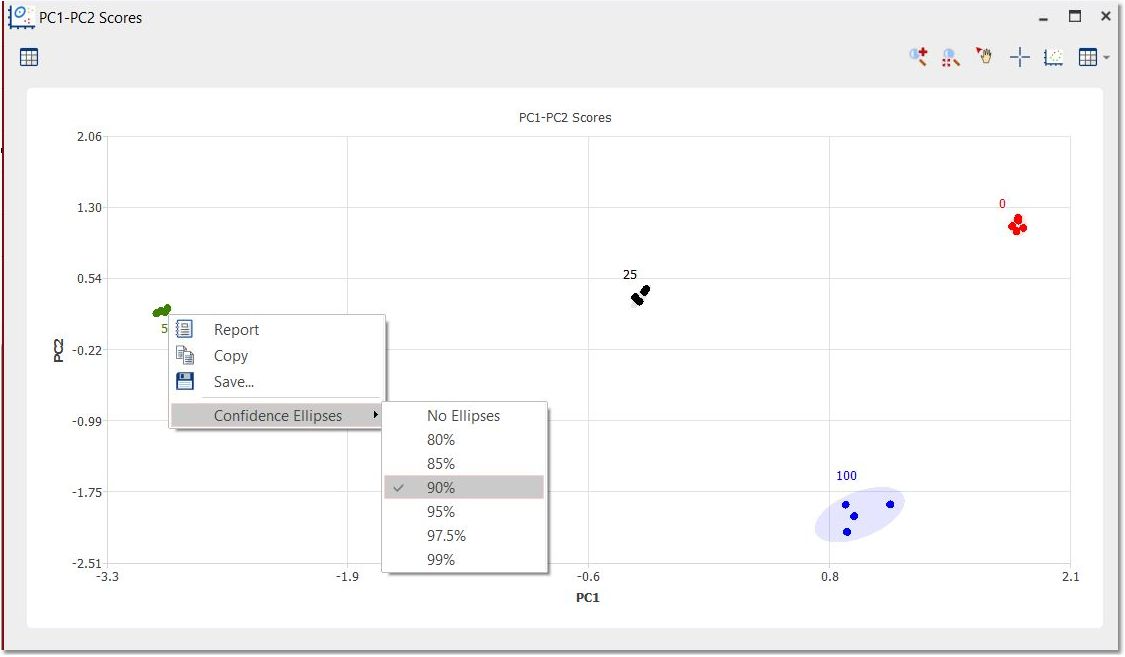
右击并选择所需的置信度值,即可显示置信度椭圆:
有关如何获取该值的详细信息,请访问此链接。
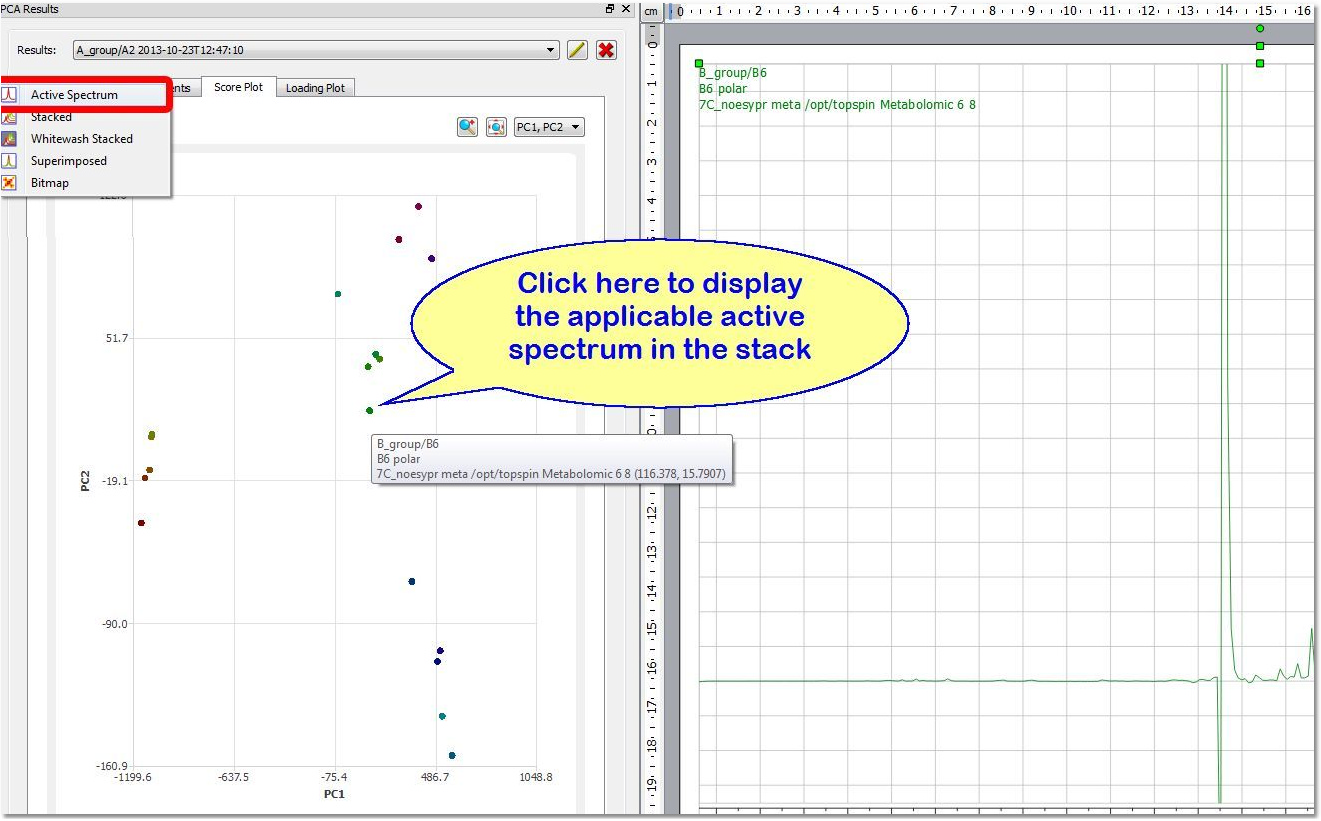
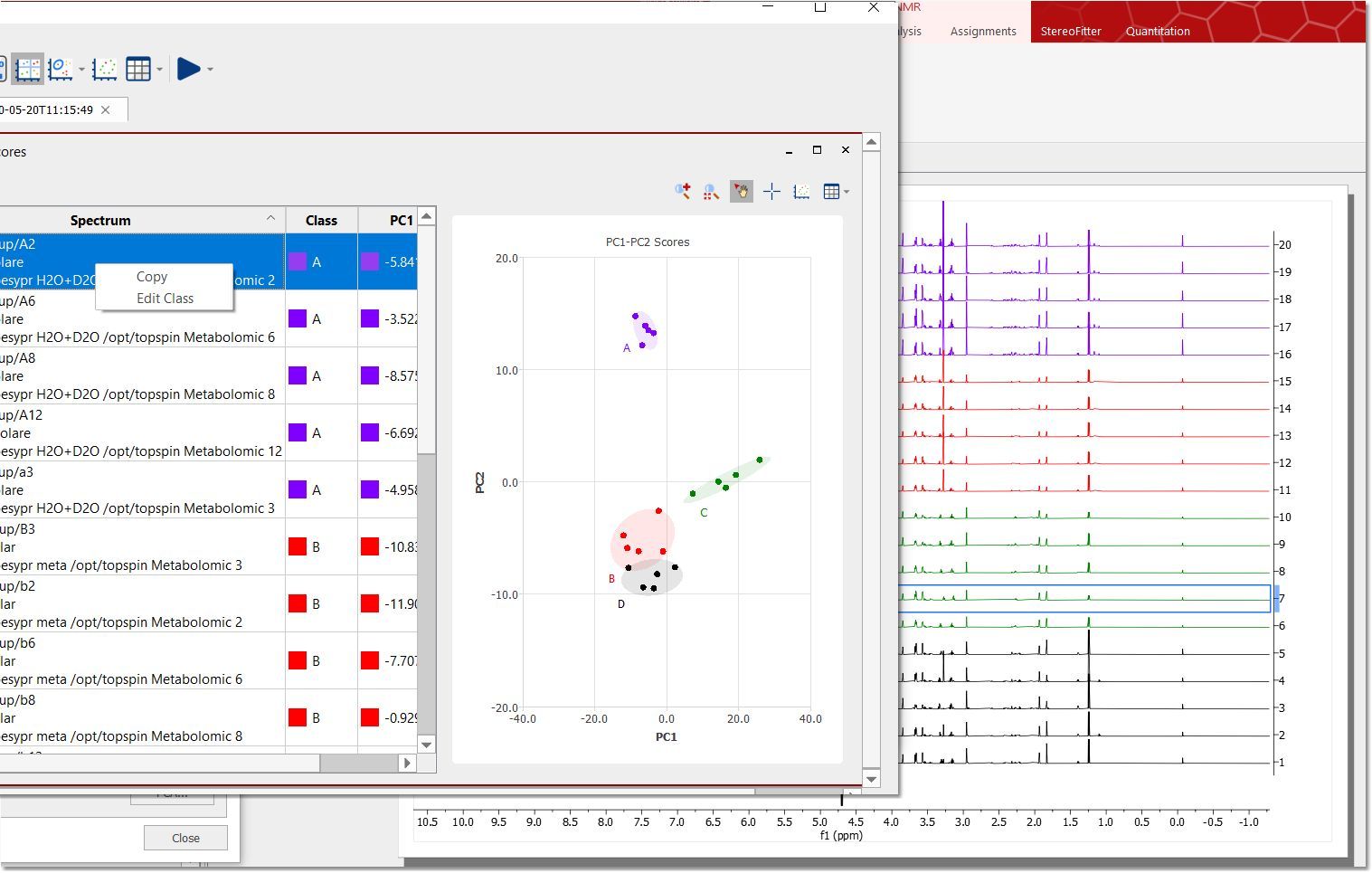
得分图 "的每个点都与堆栈的一个轨迹相关联。如果您处于 "活动频谱 "模式,点击(得分图)上的点时,将显示适用的频谱:
通过使用相应的按钮,您可以 "放大"、"重置缩放"、使用十字准线或显示载荷图。
点击 "显示表格 "按钮
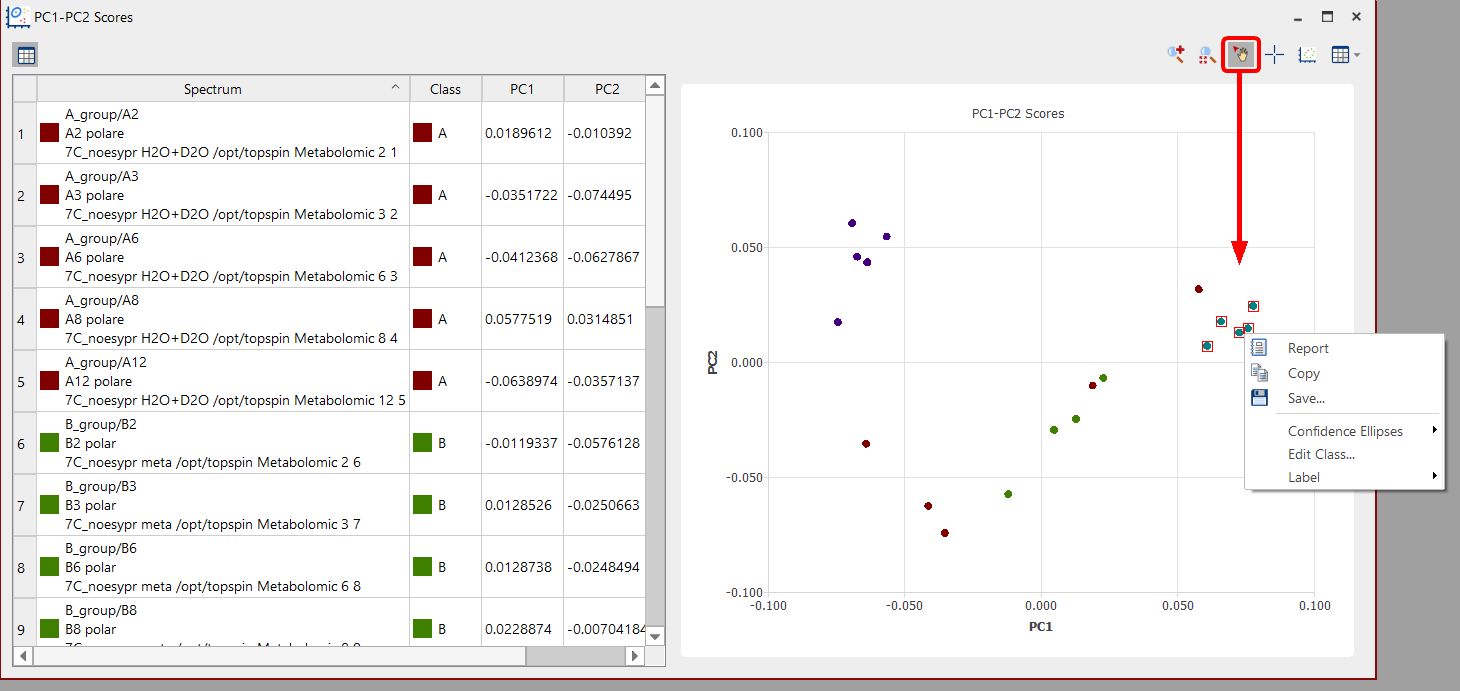
您还可以点击 "选择点 "按钮,按住 shift 键点击感兴趣的点,然后右击这些点来选择置信度、编辑类别或显示标签:
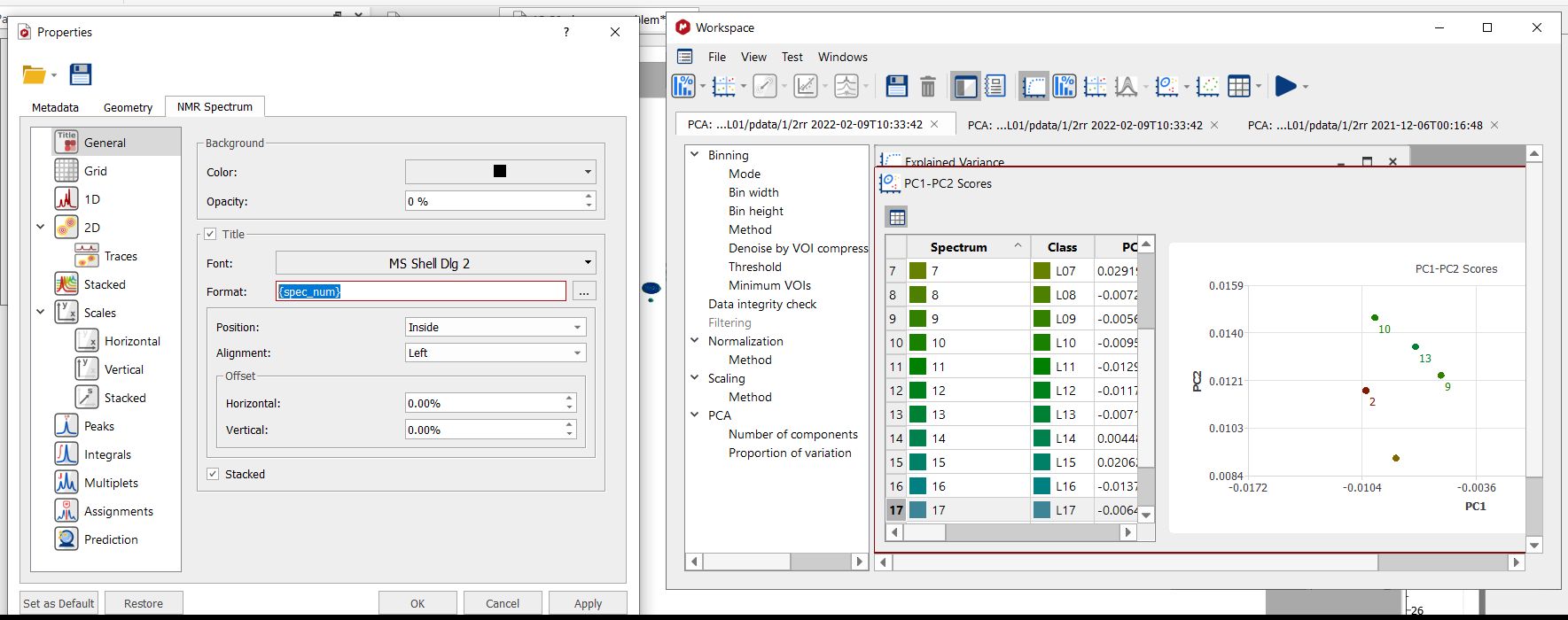
可以在该标签中显示波谱编号,但为此需要配置堆栈中波谱的标题(通过属性对话框),以便在第一行显示波谱编号:
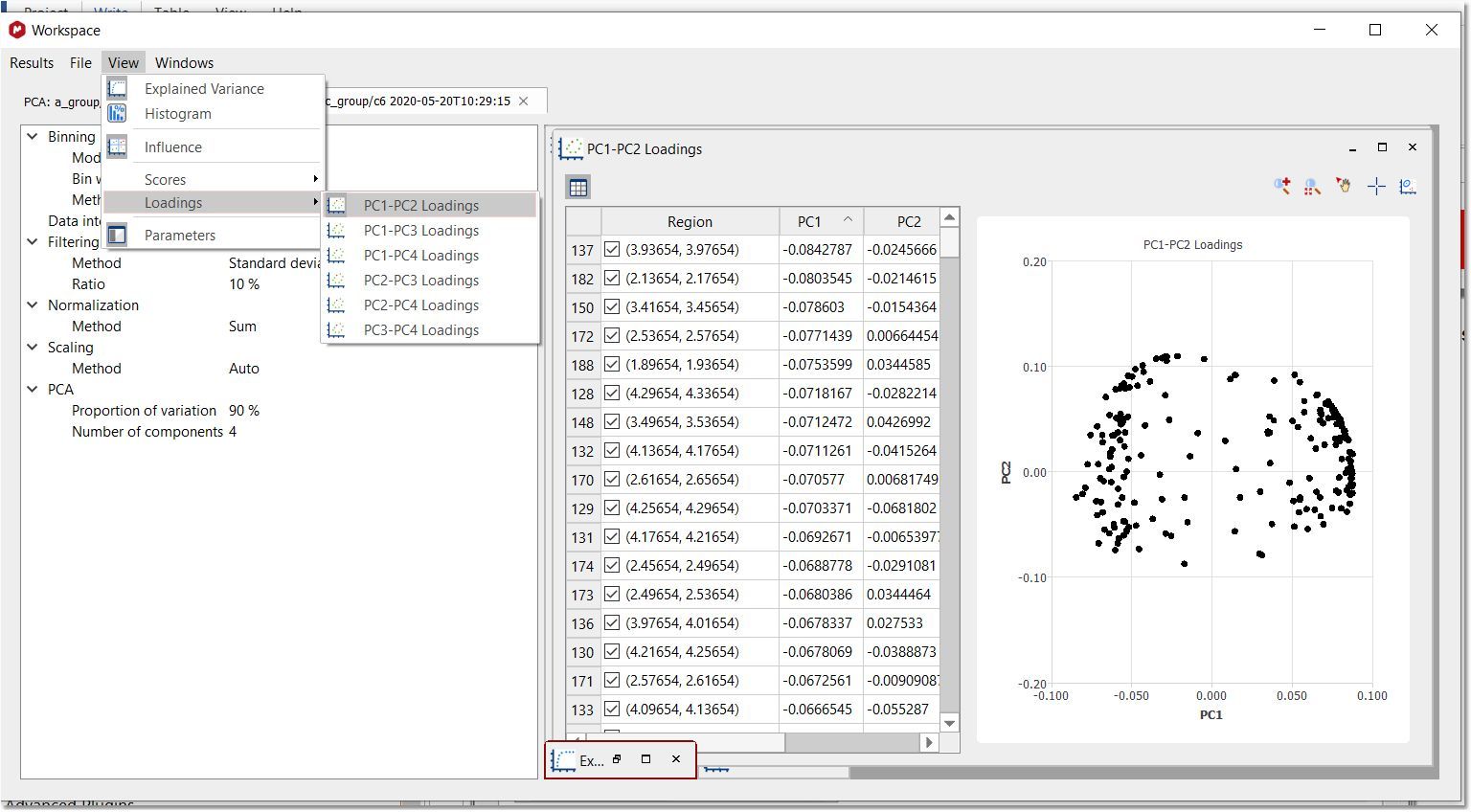
从 "视图 "菜单中选择相应的 "加载图",或点击 "分数 "面板上的相应按钮:
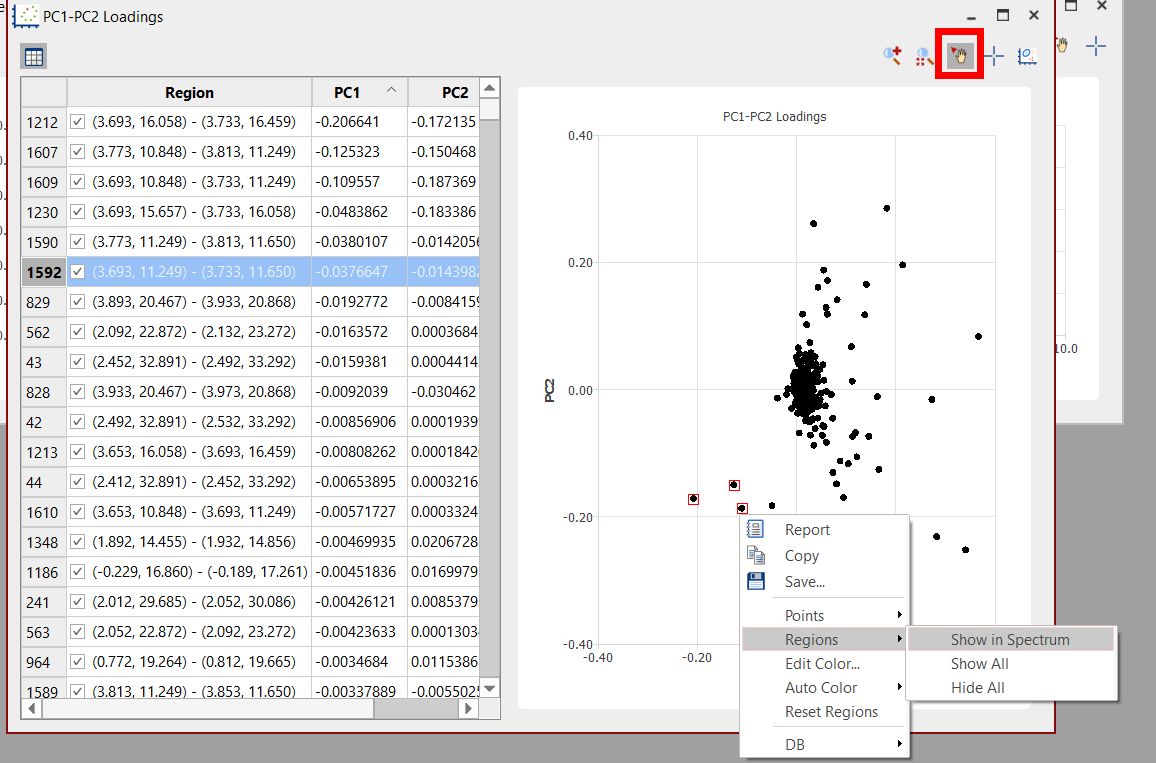
在该图中,每个点都与堆叠波谱的每个区域相关联。您可以通过右键单击相应行来更改分区的可见性和颜色:
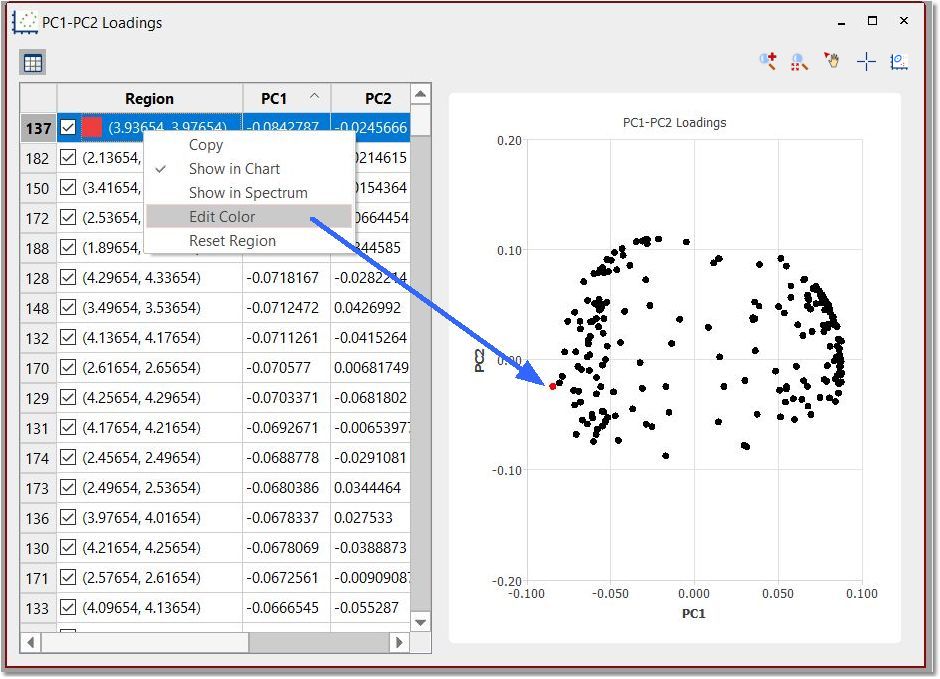
使用加载图中的 "选点 "功能并右击这些点,可以显示波谱中的区域或编辑其颜色。选择 "重置区域 "可将所有区域显示为黑色。
在右键菜单中点击 "保存 "选项,可以将结果导出为图片(png、svg、jpg 或 bmp)。
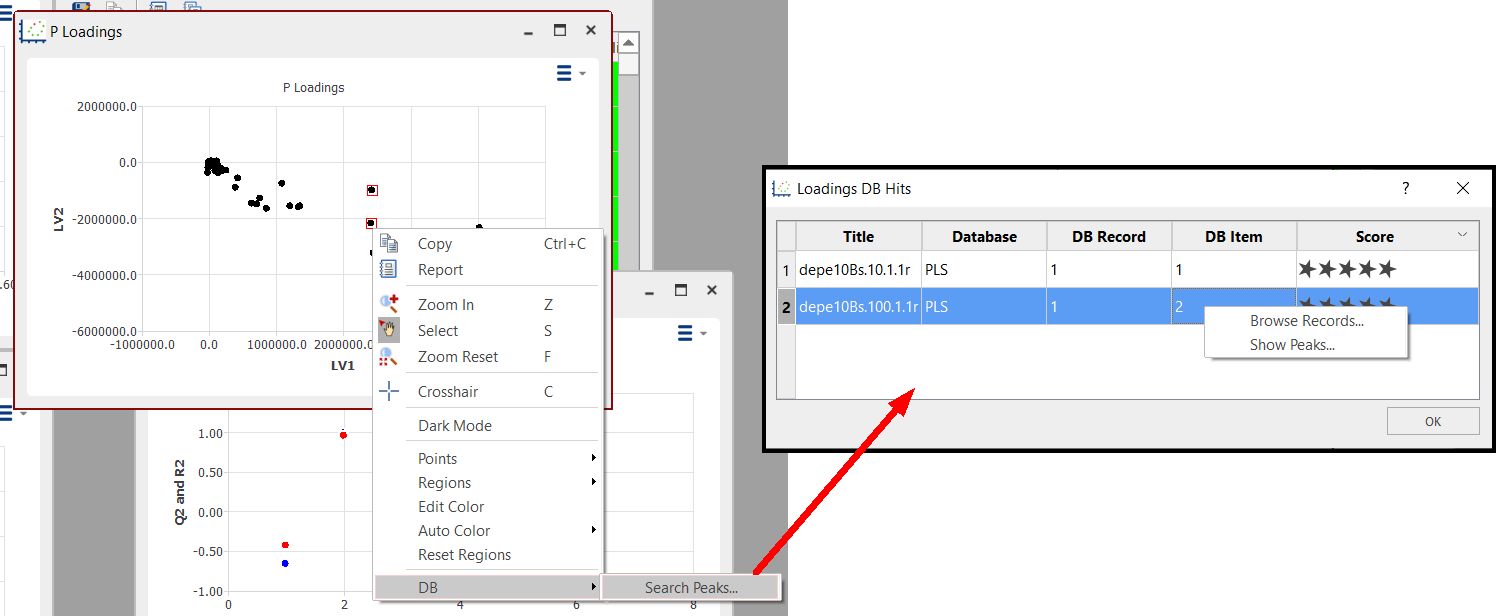
点击数据库滚动菜单,在数据库中搜索峰值:
双击一行可在数据库浏览器中显示记录。通过选择行、右键单击并选择 "浏览记录",可显示多行中的多条记录。
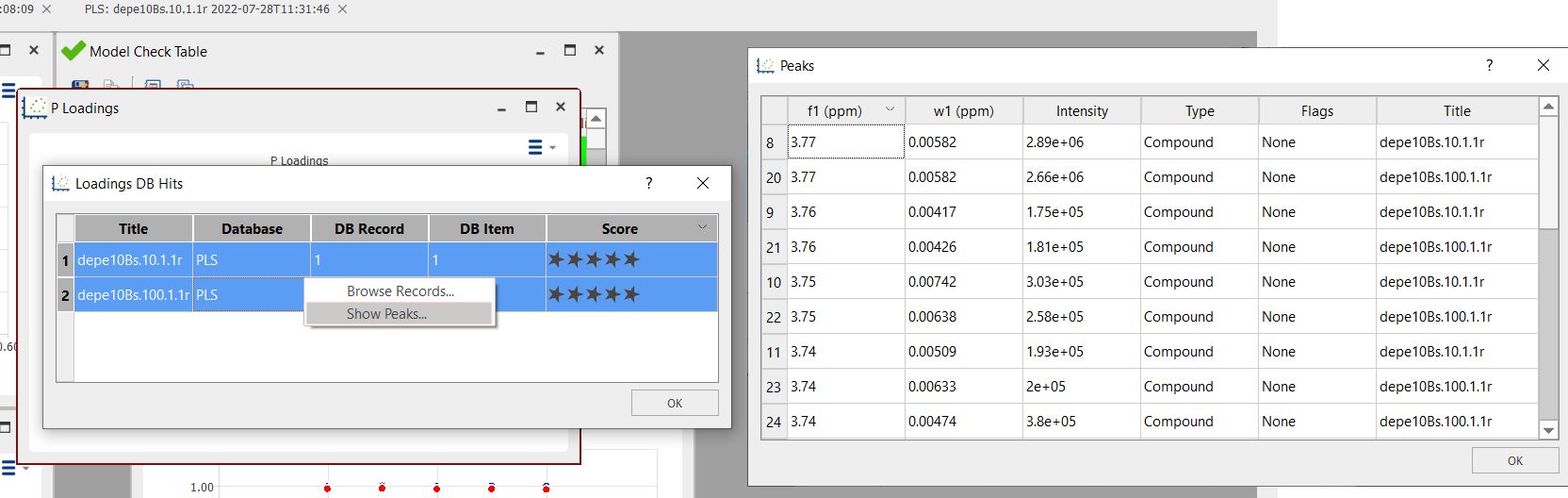
您还可以通过右键单击并选择 "显示峰值 "来显示找到的峰值列表:
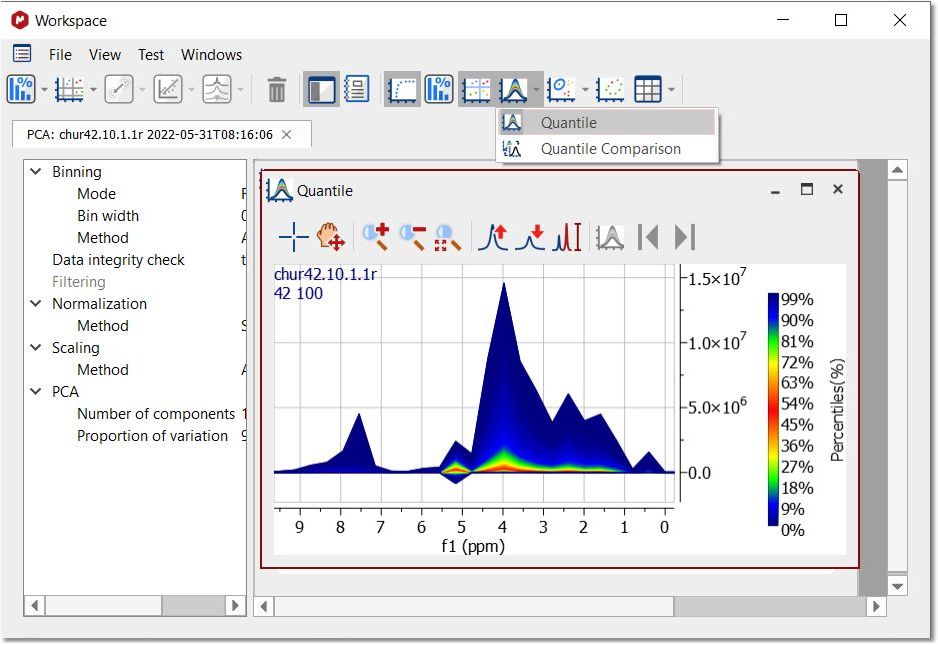
运行 PCA 后,只需点击相应的按钮,即可得到量值图:
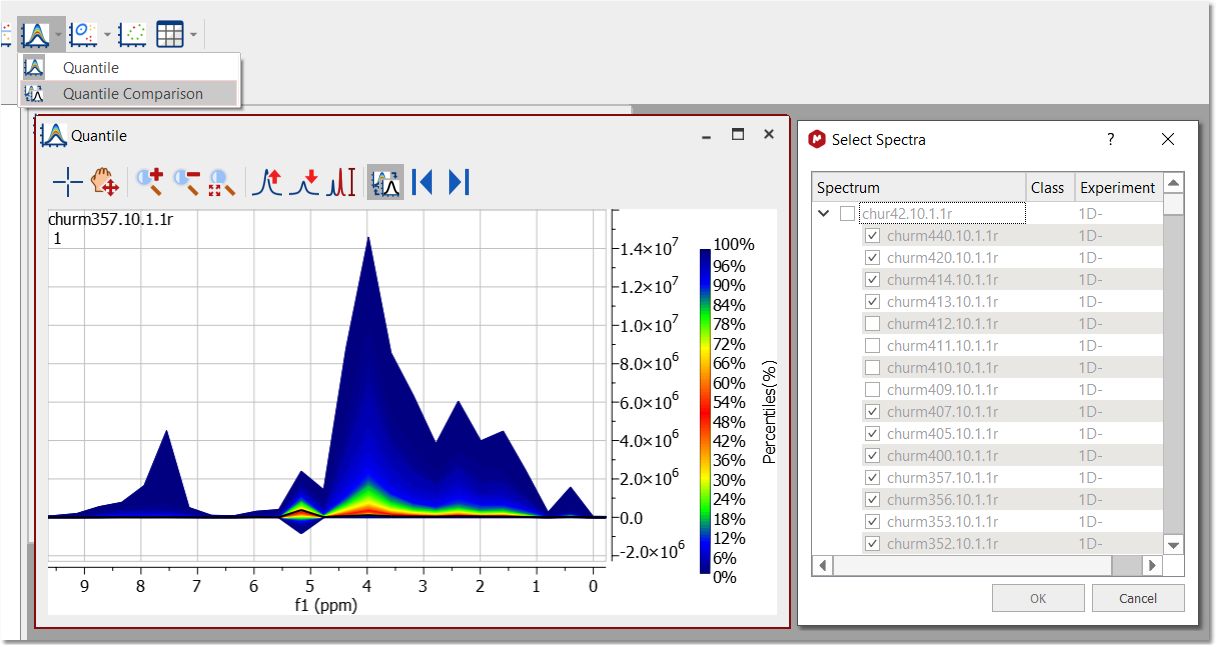
量值比较可在量值下拉菜单中找到。在这里,您可以选择堆栈中的部分或全部波谱,逐个叠加到量子图中。
如果同一文档中有一个或多个波谱未包含在堆栈中,也可以选择它们在量子图中进行比较。每个叠加的波谱都显示为黑色。
在量子图的工具栏上有专门的比较按钮: 1.在量值图和量值比较图之间切换的按钮。 2.上一个/下一个比较波谱(快捷键:SHIFT+down 和 SHIFT+Up):当选择多个波谱进行比较时,可以通过单击这些按钮浏览波谱。
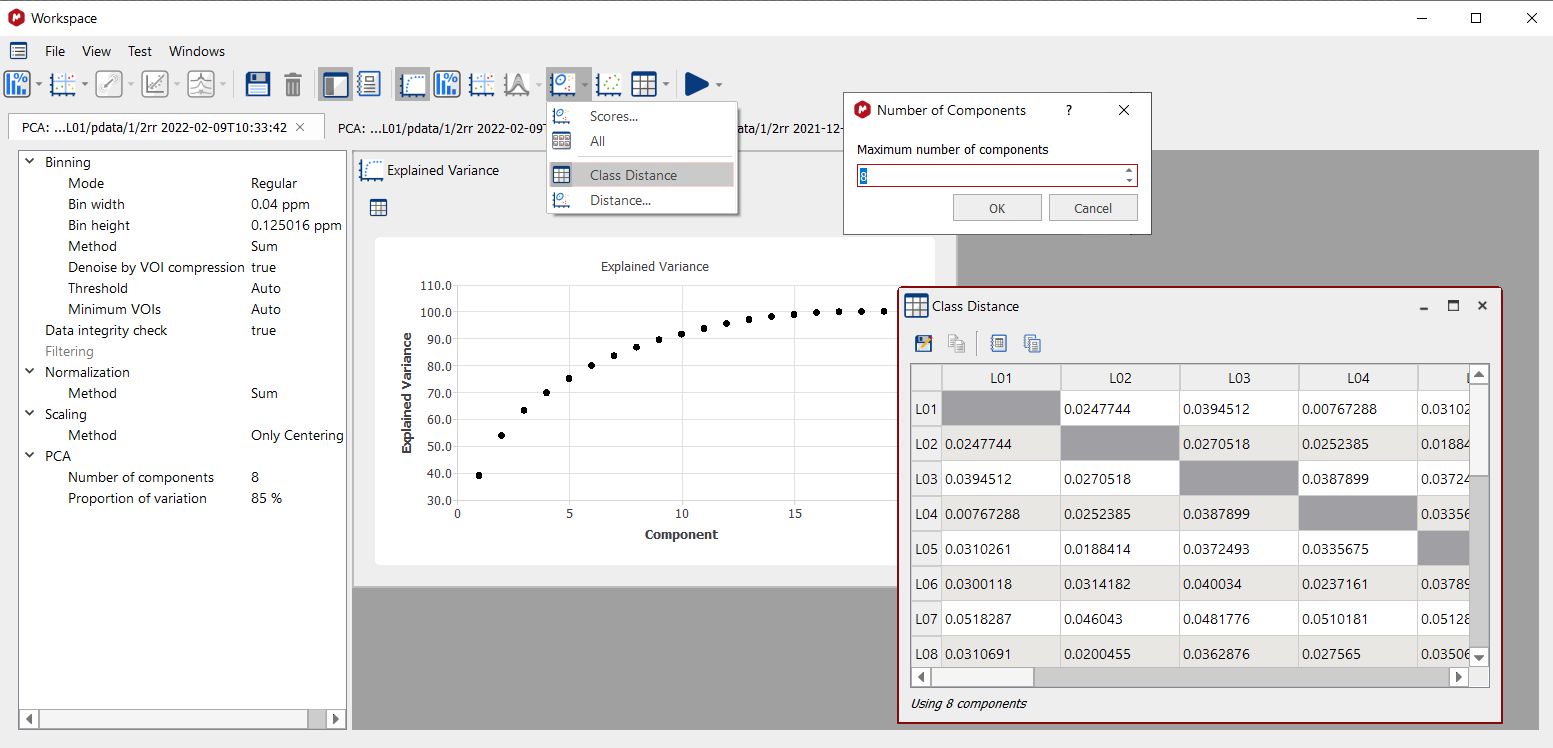
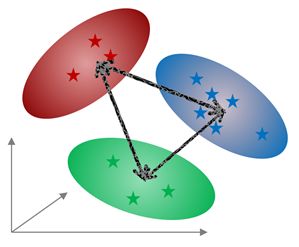
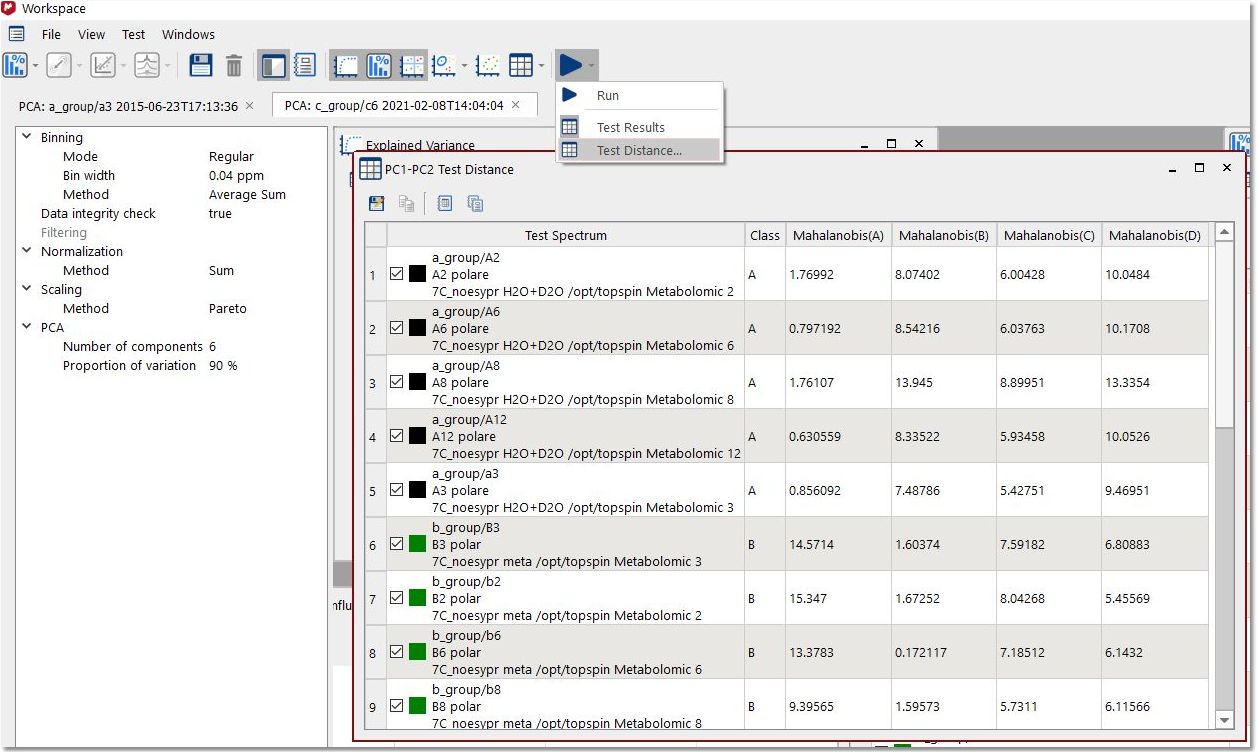
距离计算 Mahalanobis 距离描述了一个点与分布平均值之间的标准差。距离可在类之间或类与单个频谱之间计算。 为了比较类别,一旦您在一次实验中定义了多个类别,距离值越小,就表示这些类别 "越相似"。选择特征后,将显示一个新的对话框来选择要使用的成分数量(最大数量为成分总数,本例中为 8):
全局类距离是使用选定的主成分数或两个选定的 PC 从多维椭球计算得出的。
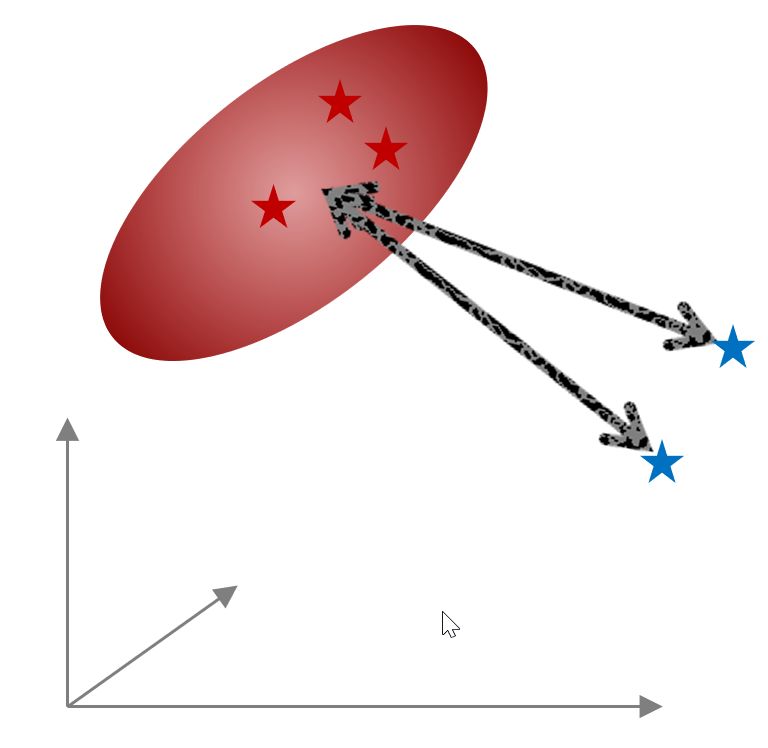
在第二种情况下(将测试波谱与不同类别进行比较),一旦运行了 PCA 并定义了类别,就可以 "测试 "一个(或多个)新波谱,将 Mahalanobis 距离与每个类别进行比较(以获得关于相似特征的信息)。
可以测量类别与单个波谱之间的距离。波谱可以取自任何加载的文档。它可以检测波谱属于哪个类别。
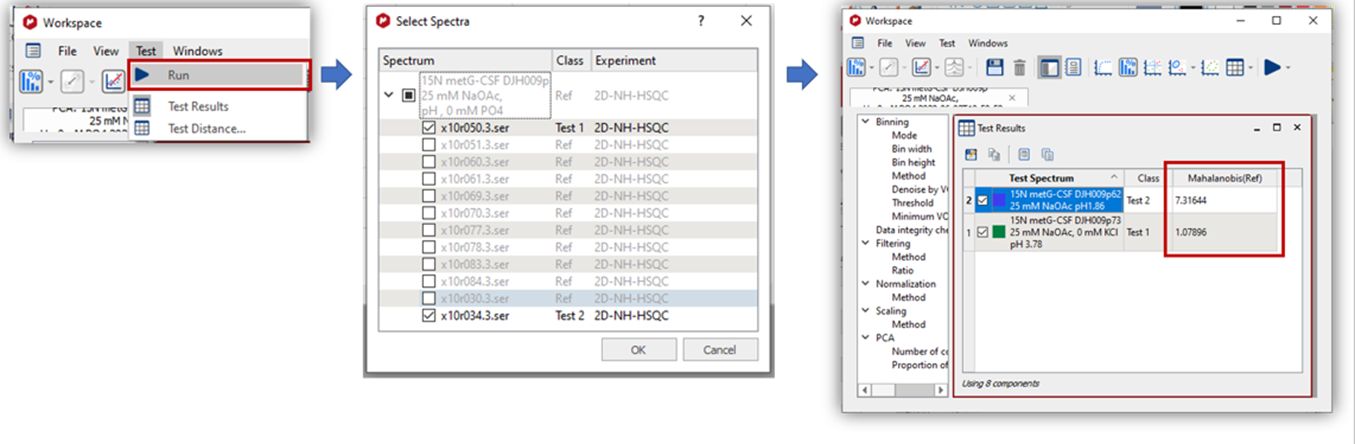
可通过 运行 命令进行计算 。可以选择单个波谱。
对于每个波谱都属于自己类别的情况,距离不是 Mahalanobis 距离,而是欧几里得距离。 更多信息请参见本文http://dx.doi.org/10.1208/s12249-017-0911-1。
另请参阅这篇有用的文章: http://nmr-analysis.blogspot.com.es/2014/01/chemometrics-under-mnova-9-pca.html http://nmr-analysis.blogspot.com.es/2014/07/pca-and-nmr-practical-aspects.html http://mestrelab.com/blog/pca-of-nmr-data-advantages-of-an-integrated-approach/ 以及这段视频:
|