Data Analysis Quick Start Guide

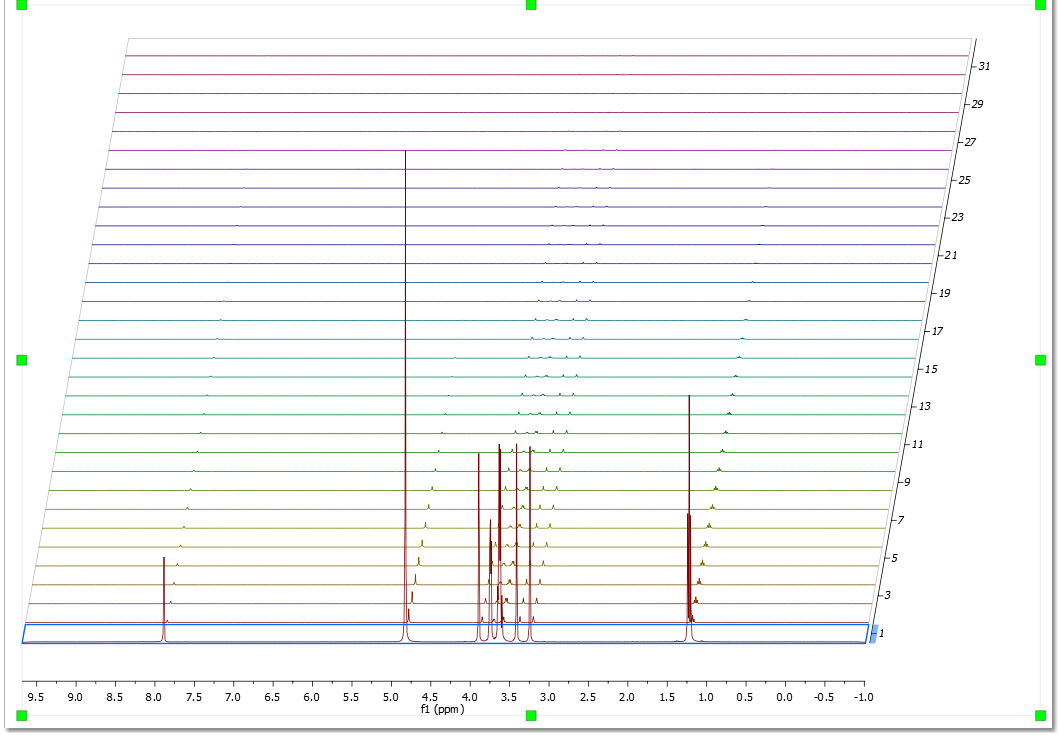
首先，请确保您熟悉堆叠图。请参阅本章 了解更多信息。

让我们来看看数据分析功能是如何工作的。只需将实验加载到 Mnova 中即可：

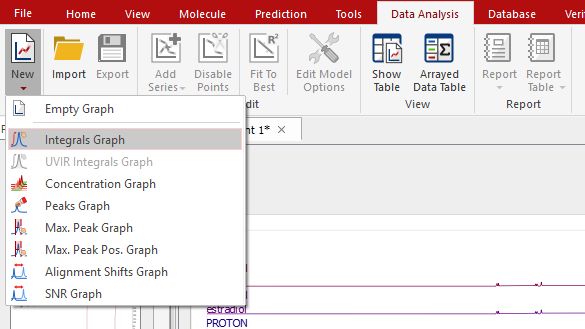
按照菜单 "Data Analysis/New（数据分析/新建）"，选择所需的图形表示法。在这种情况下，请选择 "积分图"：

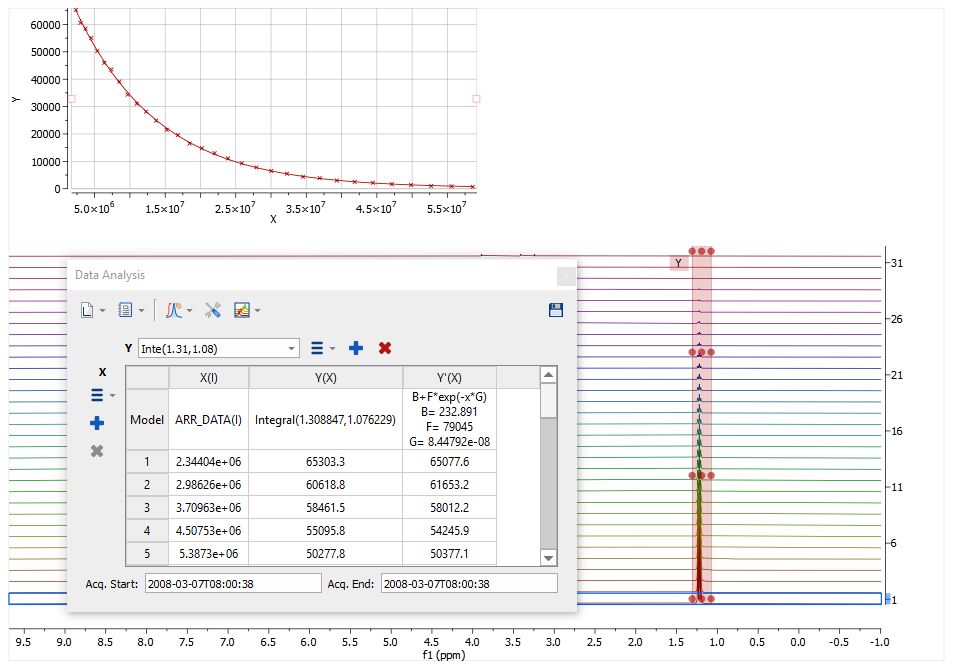
您会注意到光标将变为蓝色积分。现在您只需对所需信号进行积分（在本例中，我们将选择 1.20 ppm 处的信号）。对所需区域进行积分后，您会发现图形会随着信号的衰减而变化。请注意，所有数值都将以表格形式显示在数据分析面板中

注意：数据分析中使用的积分计算方法将是在 "积分选项"（Analysis/Integration/Options）中所选的方法。

最后，请允许 Mnova 尝试猜测反应顺序，将数据拟合到标准方程并比较均方误差。只需按照菜单 "数据分析/编辑/拟合最佳值 "进行操作即可。

您也可以在 "编辑模型选项 "中选择 "拟合函数=最佳拟合"，默认设置 "拟合至最佳 "选项。

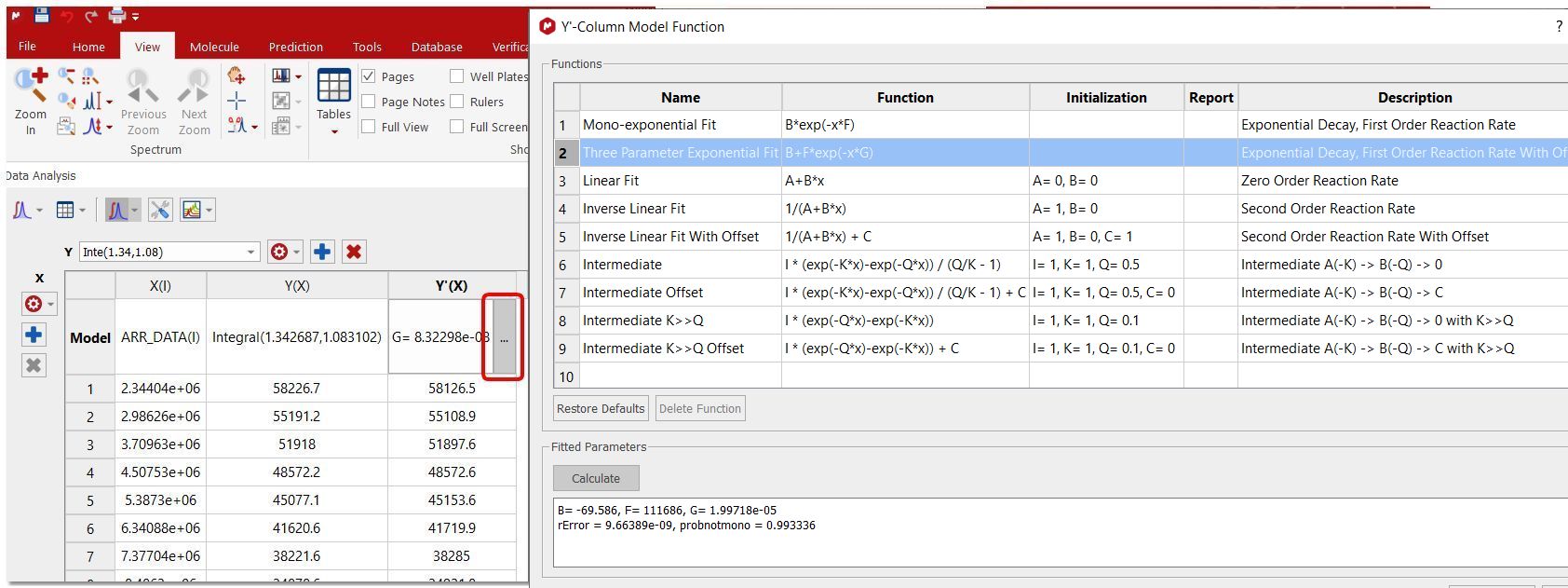
您可以在 "数据分析 "面板 （数据分析/显示表格）中找到拟合结果 。在这种情况下，最佳拟合是 "三参数指数"。如果对拟合结果不满意，只需点击Y'(X)列的第一个单元格即可选择其他函数：

注意：Probnotmono 值对于评估我们假设的拟合模型（本例中为三参数指数模型）是否满足要求非常 重要。例如，如果您假设的是单指数模型，但实验数据遵循双指数或多指数行为，那么分析将不完全正确。

另一方面，如果我们假设模型是单指数模型，"rError "值给出了 "r "值的[绝对]可能误差，其中 "r "为

y = a*exp(-r*x)+b

该误差的计算基于这样一个假设，即最终残差与数据中的实际噪声相对应。