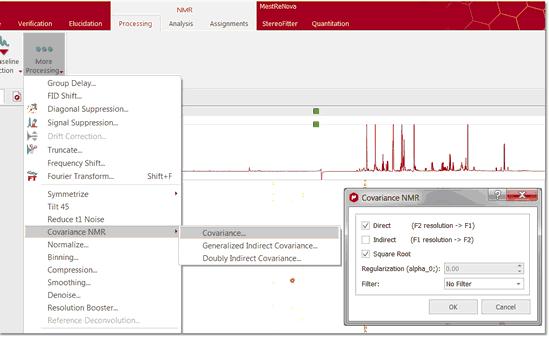
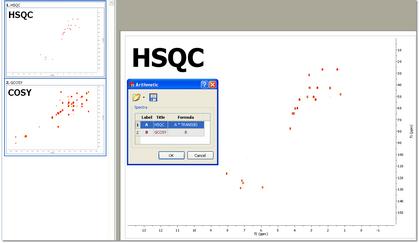
(不适用于 Mnova Lite) 分辨率和灵敏度是 NMR 波谱的两个关键因素。就二维 NMR 而言,直接维度的分辨率 (f2) 除其他因素外取决于获取的复点数,而间接维度的分辨率 (f1) 则与增量数(或获取的 FID 数)成正比。一般来说,可以说直接维度的分辨率是免费的,因为增加数据点的数量不会显著增加实验的采集时间。然而,增加 t1 数据点的数量(增量)会直接影响实验的长度,这一点可以从二维 NMR 图谱的总采集时间中看出: T = n*N1*Tav 其中,n是每个 t1 增量的扫描次数,N1是 T1 增量的次数,Tav是一次扫描的平均长度。 这通常意味着间接维度 f1 的分辨率要低于 f2 的分辨率。 您只需按照菜单 "Processing/More Processing/Covariance NMR/Covariance"(处理/更多处理/共变 NMR/共变),即可轻松应用共变 NMR 工具。这将显示 "协方差 NMR "对话框,允许您选择 "正则化因子"、"滤波器 "和 "间接协方差 NMR"。有关 CoNMR 选项的更多信息,请查阅本文:JBiomolNMR (2007) 38, 73-77
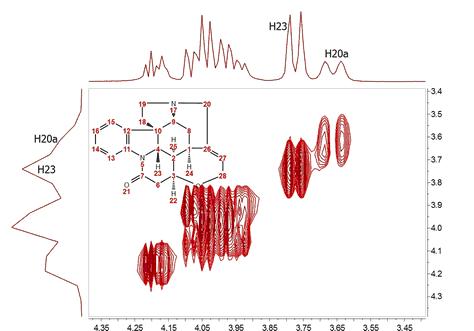
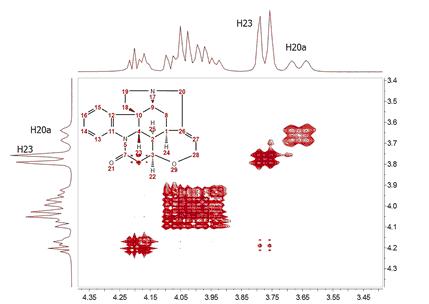
例如,让我们来看看马钱子碱的 COSY 波谱(幅值模式),该波谱是在直接维度上以 1024 个数据点和 128 t1 增量获取的。我们可以清楚地看到,沿 F2 方向的分辨率远高于沿 F1 方向的分辨率。 您可以很容易地看到,与质子 H20a 和 H23 相对应的双特在 F2 中得到了解析,而在 F1 中却没有。
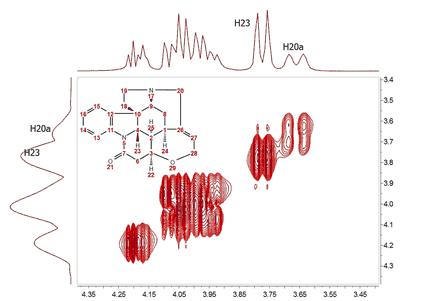
如何改进?我们可以尝试将 FID(以某种方式)沿柱(F1)外推到更高的点数(如 1024 点)。一种众所周知的技术就是简单地添加零点,这个过程被称为 "填零",基本上等同于一种频域插值。例如,在这种特殊情况下,我们可以尝试将沿 t1) 的 FID 从 128 个点外推至 1024 个点,以便与沿 f2 的点数相匹配:
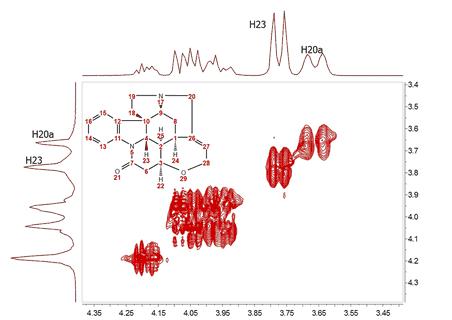
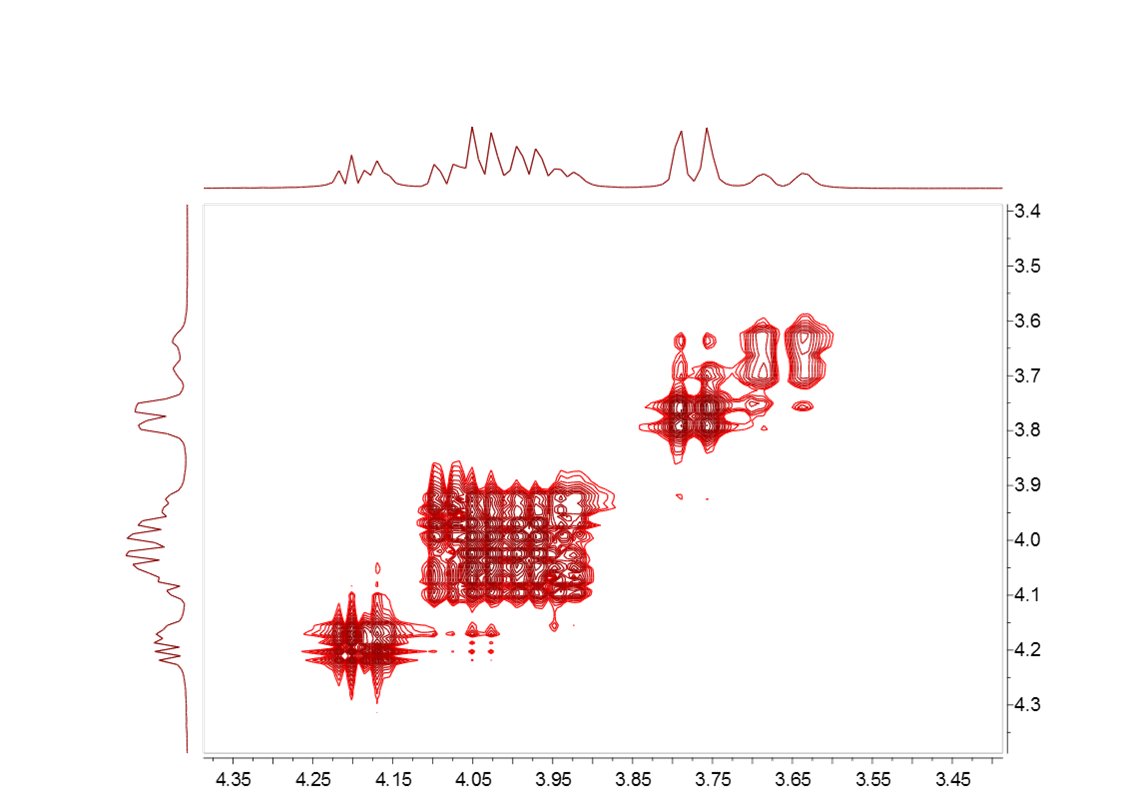
现在可以看到,沿 f1 方向的分辨率略高于前一种情况,但我们仍然无法观察到多重子(如 H20a 和 H23)的内部结构。零填充当然是一种提高分辨率的好技术,但它无法从不曾存在的地方发明新的信息。在本例中,我们对 128 到 1024 个数据点进行了零填充(例如 4 倍)。从理论上讲,我们强烈建议将零点填充至少增加两倍,因为这样可以加强因果关系,但除此之外,分辨率的提高纯粹是表面现象。我们可能会在每赫兹获得更多的数据点,但并没有获得新的信息,如上图所示。 有没有更好的方法来推断 FID?有,答案显而易见:线性预测。简而言之,前向线性预测就是利用获取的 FID 中包含的信息来预测新的数据点,这样我们就能以一种比 "零填充 "更自然的方式人为地扩展 FID。当然,我们无法通过这一过程创造出新的信息,但产生的频谱会更好看。下图对此进行了说明:
在本例中,我们将 t1-FID 从 128 个数据点扩展到 512 个数据点,然后将零填充扩展到 1024 个数据点。现在,我们可以看到 f1 线变窄了,但耦合还无法解析。 近年来,人们对开发新的方法来节省时间和处理二维(一般为 nD)核磁共振数据产生了浓厚的兴趣。事实上,协方差 NMR 有多种类型:直接、间接协方差 NMR(还有第三种方法,即不对称间接协方差,可视为间接协方差 NMR 的一种子类型)。在本手册中,我们将只介绍第一种类型,即直接协方差 NMR,其他两种类型将留待以后的教程中介绍。 在进一步了解协方差 NMR 之前,让我们来看看将此技术应用于相同频谱的结果。这就是我们得到的结果:
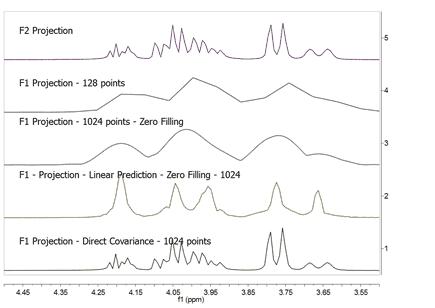
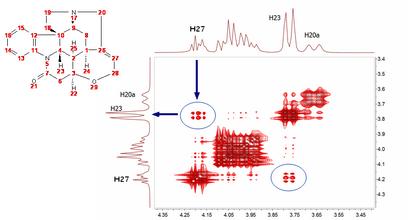
乍一看,这个结果就像是一种魔法:现在,H20a 和 H23 的分裂在两个维度上都得到了清晰的解析。实际上,F1 维度的解析度与 F2 维度的解析度类似。 从直观的角度来看,我们在这里取得的成果是将 F2 维的分辨率转移到了 F1 维。换句话说,我们采用了一种数学方法,利用 F2 维度的较高波谱分辨率,将其转移到 F1 维度。 在数学上,直接协方差 NMR 非常简单,其定义公式如下: C = (FTF) (1) 其中,C 为对称协方差矩阵,F 为常规二维 FT 频谱的实部,FT为其转置(注:直接协方差 NMR 也可应用于混频-时域,即频谱沿 F2 变换时。在这种情况下,不需要第二个 FT,也不需要在间接维度上进行光度或相位校正)。 为了将协方差频谱的强度近似为理想化二维 FT 频谱的强度,应取 C 的平方根。平方根还可以抑制FTF中由于共振重叠而产生的错误相关性。C 矩阵平方根的求取实际上是使用标准线性代数方法(简而言之,将矩阵对角化,然后使用特征向量和特征值平方根重建C1/2)完成的。 因此,直接协方差 NMR 能够产生二维频谱,其中两个维度的分辨率由直接维度的频谱分辨率决定。 让我们来看看堆叠图的表示方法,它包含了从此处描述的不同处理方法(零填充、线性预测和直接协方差 NMR)中获得的一维投影。您可以在下图中看到协方差 NMR 方法的威力。
协方差 NMR波谱法可在间接维度上提供最大分辨率,但当获取的数据点数量太少时,协方差会表现出不良的统计特性,表现为虚假的交叉峰。例如,在这种情况下,我们可以看到一些意想不到的交叉峰(如相关的 H27 和 H23,原则上不应该出现在 GCOSY 波谱中,而应该出现在 TOCSY 波谱中)。当不同自旋系统的质子与具有重叠质子多重子的共振耦合时,也可能会出现一些其他伪影。
Mnova 包含一个新颖的滤波器来解决这种情况。该滤波器将标准的二维 FFT 频谱与 CoNMR 版本结合起来,这样得到的频谱在保持 F1 的高波谱分辨率的同时,还不会产生伪影:
间接协方差核磁共振 有趣的是,如果我们有一个异核谱,只需改变乘法的顺序,就能将相关信息从间接维度转移到直接维度: 例如,下面的波谱显示了蔗糖的 HSQC-TOCSY 波谱(左图)及其产生的间接协方差对应图(右图),其中包含的自旋连接信息与直接 13C 检测的 13C-13C TOCSY 基本相同:
非对称协方差 NMR 您还可以使用 Mnova 进行非对称协方差 NMR 。不过,与只需处理单个频谱的直接/间接协方差 NMR 相比,非对称 NMR 处理可能并不那么直观,因为需要使用两个独立的频谱,因此我们决定采用一种非常开放和灵活的方法来实现它,即使用频谱运算模块。
使用 Mnova 应用 "非对称 CoNMR "有两种方法: 1.使用算术功能 2.使用广义间接协方差 NMR
如上所述,协方差 NMR 完全是矩阵运算。使用直接/间接共振核磁共振时,只需将频谱矩阵乘以其转置,乘法的顺序取决于共振核磁共振技术(直接与间接)。同样的概念也适用于非对称 CoNMR,您只需将一个频谱乘以另一个频谱的转置。
假设矩阵 A 对应于 HSQC 波谱,矩阵 B 对应于 COSY(或 TOCSY)波谱,非对称 CoNMR 可通过以下矩阵运算实现:
C = A * TRANS(B)
其中 TRANS 表示矩阵转置。
需要注意的是,进行任何代数矩阵运算时,矩阵 A 和 B 必须根据其行/列尺寸相匹配。
要进行非对称 CoNMR,只需在 Mnova 中打开两个单独的波谱,然后像往常一样进行处理(确保大小兼容),最后在处理/算术中输入所需的方程(例如 A * TRANS(B) )
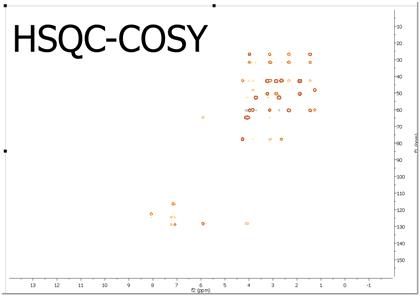
让我们逐步了解如何使用 Mnova 从单独的 HSQC 和 COSY 图谱生成 HSQC-COSY 图谱
1.将 HSQC 和 COSY 图谱导入 Mnova
2.在页面导航器中选择这两个波谱,然后按照菜单 "分析/更多工具/运算
最后输入如上所示的公式 "A*TRANS(B)"。在本例中,A 对应 HSQC 波谱,而 B 是 COSY 实验。TRANS 表示转置运算。
操作完成后,点击 "拟合到最高强度 "按钮
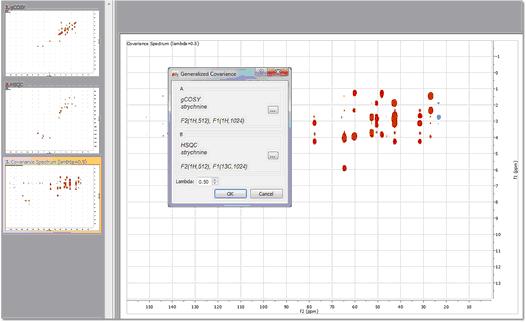
广义间接协方差 NMR (GIC) 多维核磁共振 (NMR) 实验可以测量自旋-自旋相关性,从而提供有关键连接性和分子结构的重要信息。然而,由于灵敏度和分辨率的限制,直接观测某些类型的相关性可能非常耗时。
协方差 NMR 通过计算对称协方差矩阵得出自旋之间的相关性,再通过矩阵平方根生成分辨率更高的频谱。协方差概念还被用于从具有共同频率维度的成对二维波谱重建非对称波谱。由于非对称协方差 NMR 程序缺少矩阵平方根步骤,因此无法抑制中继效应,从而可能因化学位移退化而产生假阳性信号。这种广义协方差形式允许构建非对称协方差 NMR 波谱,并可对其进行任意矩阵函数(如平方根)处理,从而改善波谱特性。
该方法与上述方法(算术)基本相同,但使用了更严格的数学形式主义,可以最大限度地减少假阳性峰的数量,因为现在用户可以使用两个矩阵乘积的平方(或 lambda 参数的任何其他值,即:0.25)。
要使用这种方法,只需加载数据集,然后按照菜单 "Processing/More Processing/Covariance NMR/Generalized Indirect Covariance"(处理/更多处理/共变 NMR/广义间接共变)进行操作。最后选择要使用的波谱,并输入 lambda 参数值。
请注意,要应用 GIC,F2 中的两个波谱必须具有相同的点数。
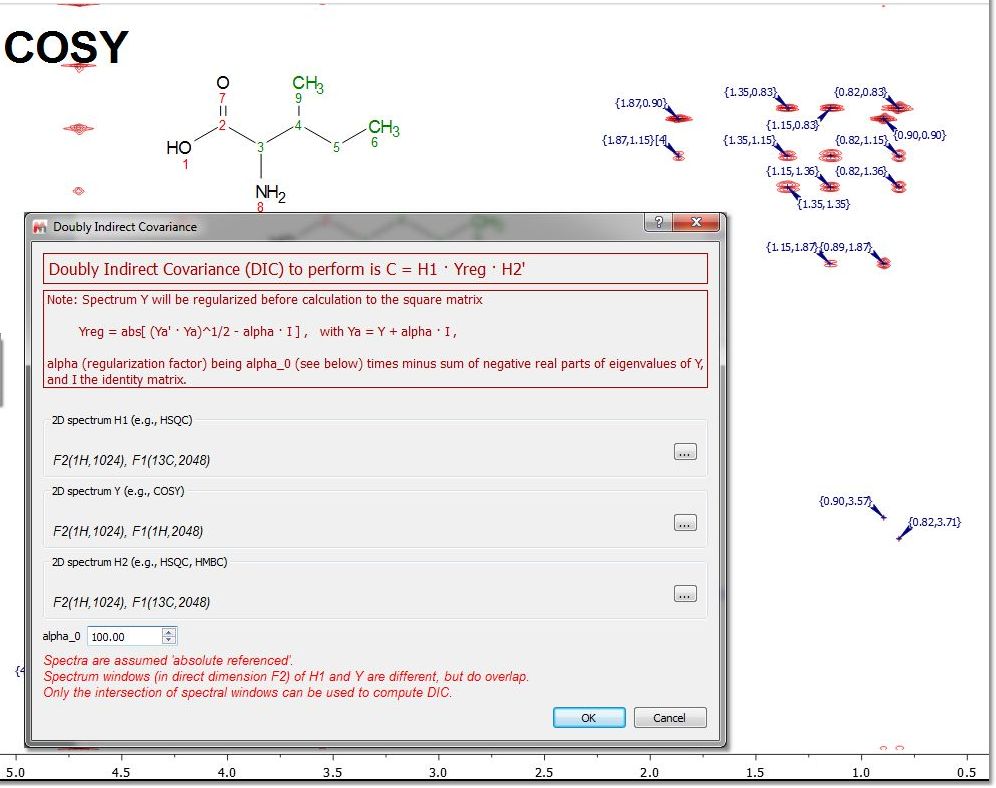
双协方差 NMR 双协方差 NMR 波谱在结构阐释方面非常有用,因为生成的波谱实际上是一张碳连接图,可以直接用基本图论进行分析,从而获得分子的骨架结构,甚至是单个混合物成分或其片段的骨架结构。 在下面的示例中,我们在同一文档中加载了 COSY 和 HSQC。
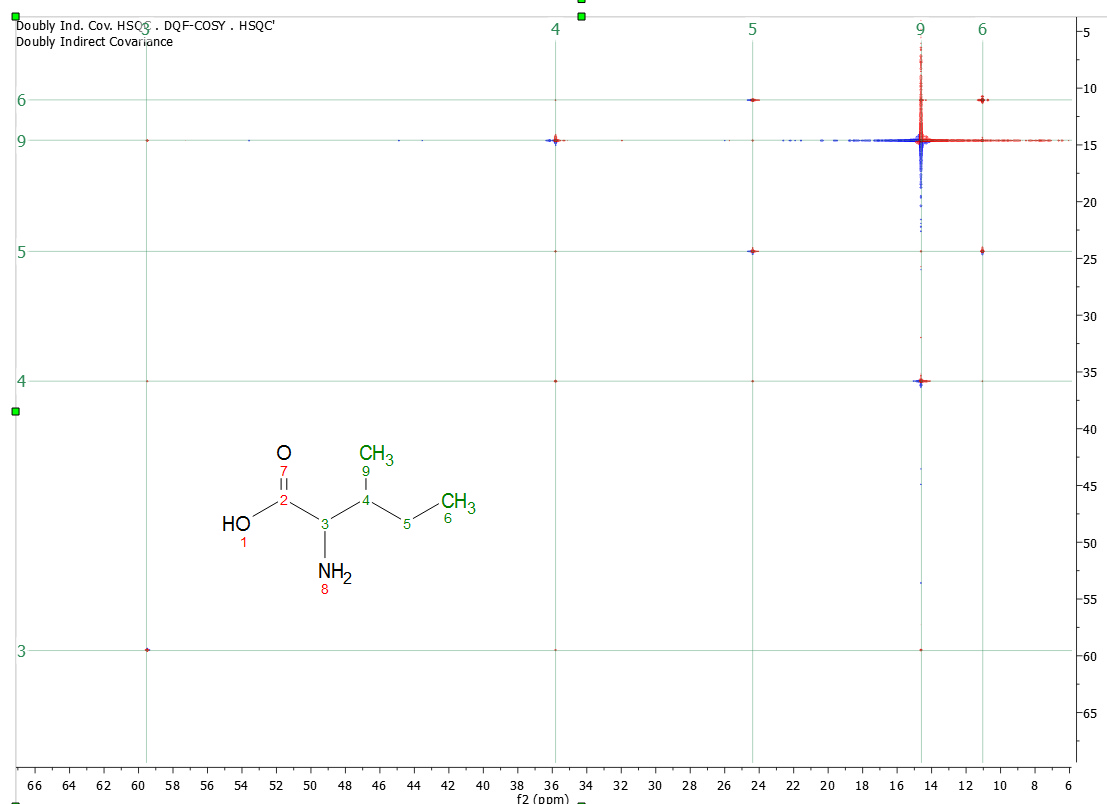
按照菜单 "Processing/More Processing/Covariance NMR/Doubly Indirect Covariance"(处理/更多处理/共变异 NMR/双间接共变异)操作后,我们将得到一个带有碳连接图的合成频谱(HSQC,HMBC):
有关 CoNMR 的更多信息,请阅读我们的博客: http://nmr-analysis.blogspot.com/2008/10/introduction-to-covariance-nmr.html http://nmr-analysis.blogspot.com/2008/11/indirect-covariance-nmr-fast-square.html http://nmr-analysis.blogspot.com/2008/11/removal-of-artifacts-in-direct.html
本评论: http://www.ebyte.it/library/docs/nmr14/2014_NMR_Cobas_Covariance.pdf 以及这篇论文:JBiomolNMR (2007) 38, 73-77
有关双间接 CoNMR 的更多信息:J.Am.Chem.Soc. 2010, 132,16922 |