DOSY/ROSY Transform

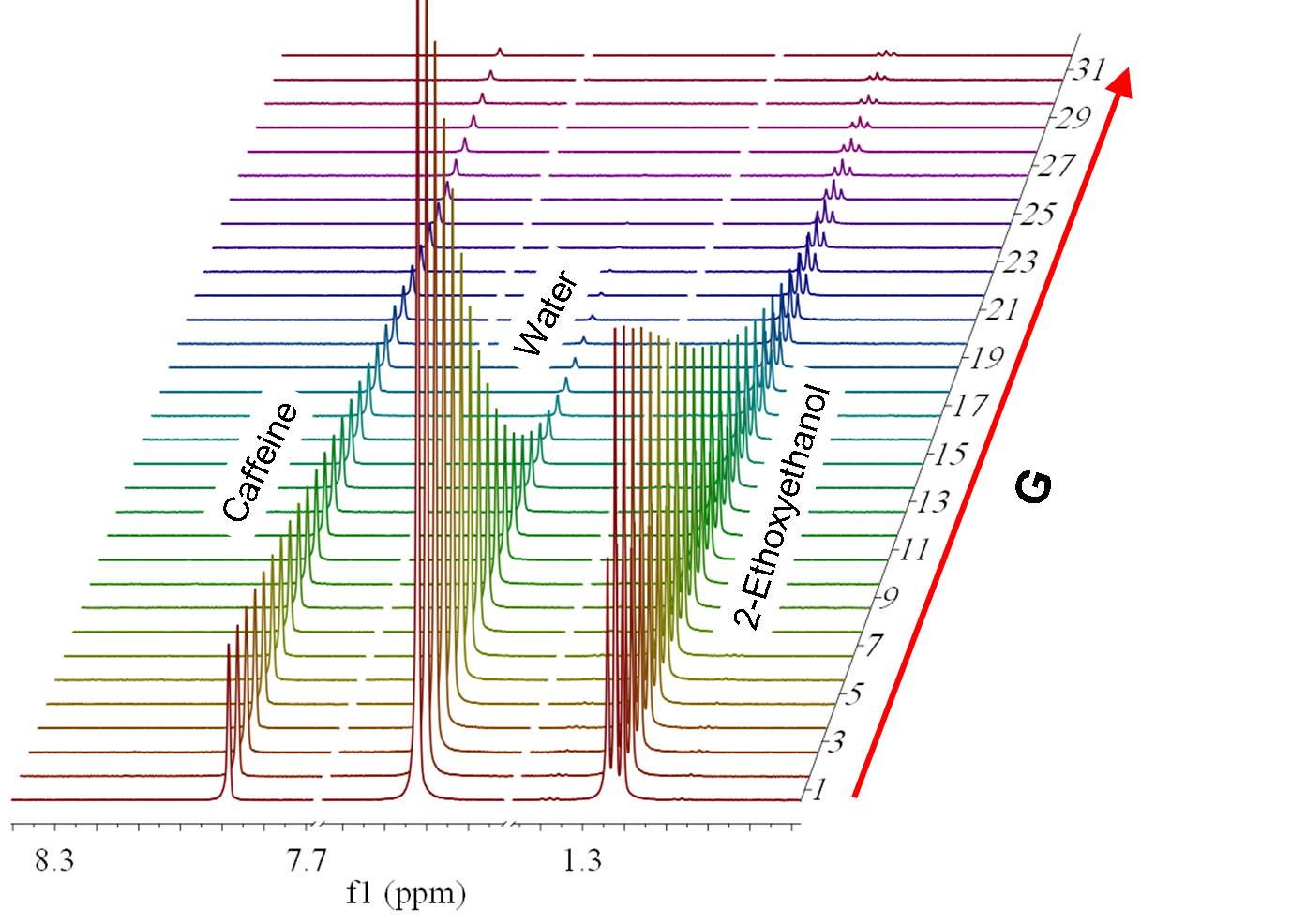
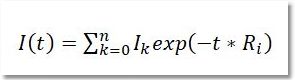(Mnova Lite 中不可用）

核磁共振扩散实验提供了一种根据溶液中每种化学物质的不同平移扩散系数（因此也包括分子大小和形状的差异，以及周围环境的物理特性，如粘度、温度等）来分离混合物中不同化合物的方法。在某种程度上，它可以被视为一种特殊的物理成分分离色谱法，但与这些技术不同的是，它不需要任何特殊的样品制备或色谱法优化，并在分析过程中保持样品的固有化学环境。

扩散测量是通过观察脉冲场梯度实验中核磁共振信号的衰减来进行的。衰减程度是磁梯度脉冲振幅 (G) 的函数，其发生率与分子的扩散系数 (D) 成正比。假设给定（固定）化学位移 f 处的谱线属于具有扩散常数DA 的单一样品成分 A，则
 
S(f,z) =SA(f) exp(-DAZ)(1)

 
其中， SA(f)是成分 A 在零梯度下的波谱强度（A 的 "正常 "波谱），DA是其扩散系数， Z则表示实验中使用的不同梯度振幅。
 
根据实验类型的不同，Z的计算公式也各不相同，包括应用梯度的振幅G和一个或多个定时参数，如 Δ （两个脉冲梯度之间的时间，与回波时间有关）和 Δ （梯度脉冲宽度）。以使用两个矩形梯度脉冲的原始 Tanner-Stejskal 方法为例、

 
Z =γ2G2δ2(Δ-δ/3) (2)

上述等式严格适用于简单的 PFG-NMR 实验，为适应更复杂的脉冲序列，可稍作修改。
 
在实践中，一系列 NMR 扩散谱是作为梯度强度的函数获取的。例如，下图显示了含有咖啡因、2-乙氧基乙醇和水的混合物的一系列 1H-NMR 扩散实验结果。
 

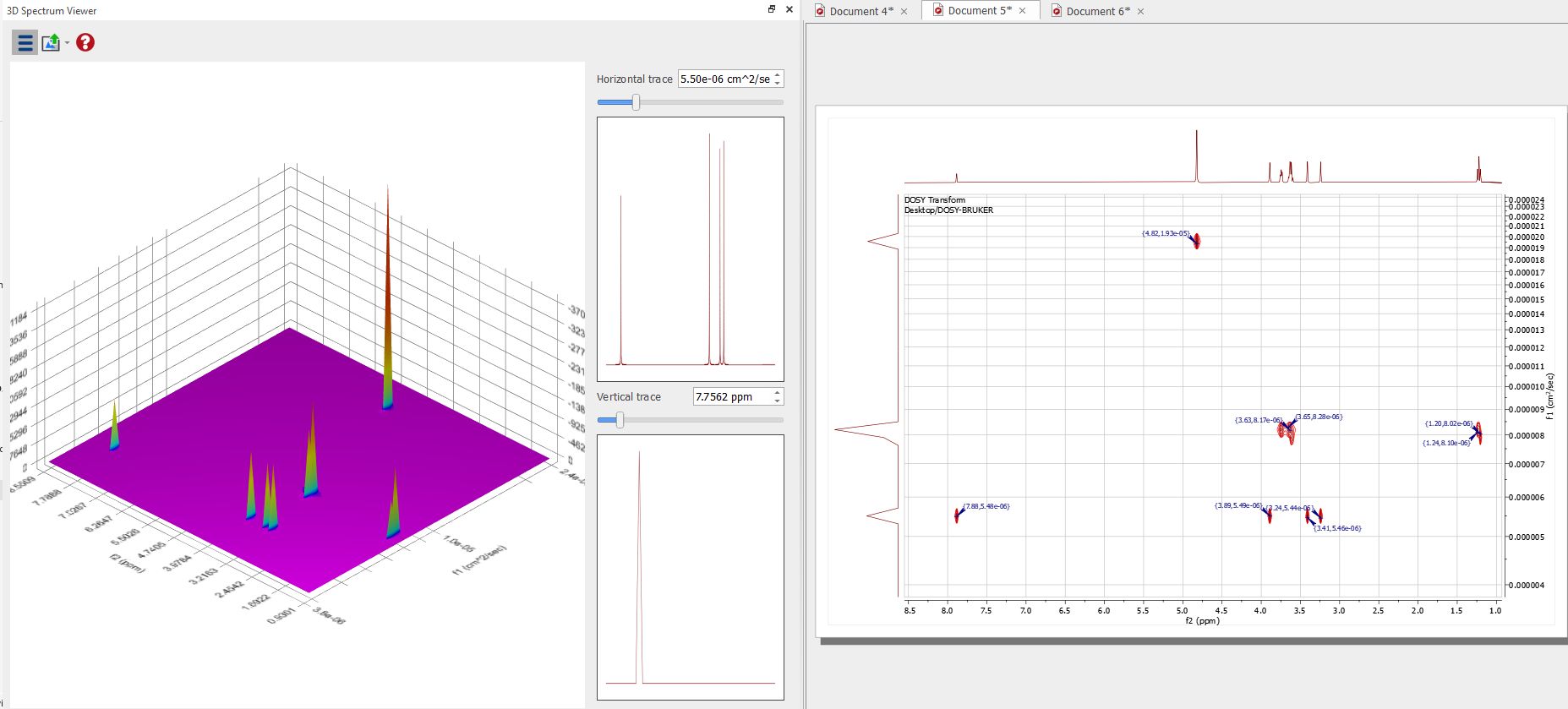
可以看出，共振频率的强度呈指数衰减。根据公式 (1)，该衰减的斜率与扩散系数成正比。与同一分子物种相对应的所有信号都会以相同的速率衰减。例如，水的峰值比咖啡因和 2-乙氧基乙醇的峰值衰减得快。

请注意，加载一维 NMR 图谱的叠加图也会在三维查看器中显示结果：

 
DOSY 转换

就原始 PFG-NMR 波谱的数据处理而言，目标是将 NxM 数据矩阵 S 转换为 NxR 矩阵（二维 DOSY 波谱），如下所示：
 

 
DOSY 图谱 D 的横轴与 S 的横轴相同，并编码所观察到的核的化学位移（一般为 1H）。垂直维度则表示扩散常数 D，这就是扩散有序波谱 NMR（DOSY）。在成分线不重叠且无化学交换的理想情况下，二维峰沿着水平线排列，每条线对应一个样品成分（分子）。
 
沿着这样一条线的水平切口应显示该成分的 "正常 "波谱。垂直切面显示的扩散峰位于定义相应扩散常数的位置。
 
S=>D的映射从此称为 DOSY 变换。遗憾的是，这种变换并不简单。实际应用包括单指数和双指数拟合、最大熵和多变量方法（如 DECRA）。
 
我们最近开发了一种全新的 DOSY 处理方法，并已将其纳入Mnova。
 

贝叶斯 DOSY 变换

让我们逐步了解这一功能的工作原理：

1.导入原始数据：例如，将波谱文件夹拖入 Mnova：

2.处理频谱： Mnova 会自动为您处理频谱。不过，可能需要进行一些进一步处理，通常是手动相位和基线校正。

您可以直接在堆叠图模式下进行处理，但建议使用 "活动波谱 "模式，如下图所示：

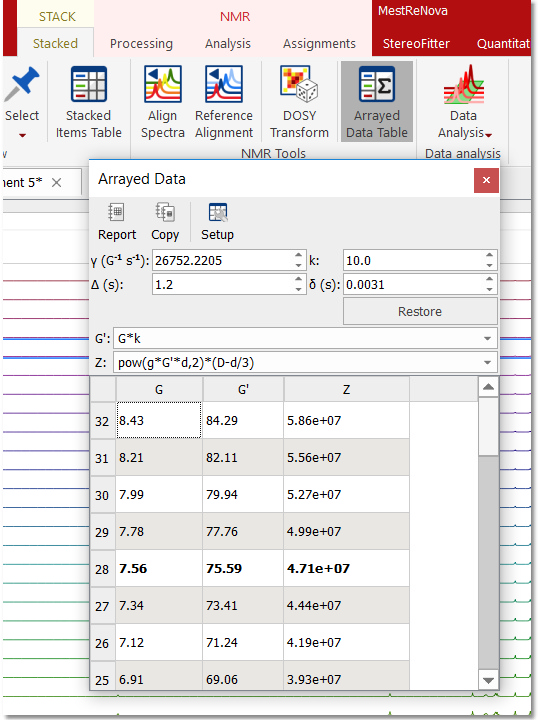
在 "活动波谱 "模式下，校正任何相位失真并应用自动基线校正（使用伯斯坦多项式）。这些校正将应用于整个数据集。如果迹线未对齐，也可以使用对齐工具（在堆叠功能区下）。

3.设置与扩散相关的指数值： 通过菜单 "View/Tables/Arrayed Data"（查看/表格/已排列数据）（或堆栈 "Arrayed Data Table"（已排列数据表）），确保从实验文件中正确读取了大三角洲值和小三角洲值。

这些数值应以秒为单位输入：

通过 BayesianDOSY 变换 (BDT)，我们可以拟合出以下类型的模型

S(f,z) =SA(f) exp(-dAz)

其中，SA(f)是零梯度时 A 组份的波谱强度（A 的 "正常 "波谱），dA是其扩散系数。第三列显示了与上述表达式相对应的 Z 值，这些值是根据图中突出显示的公式计算得出的。

假定梯度强度单位为 G/cm。请注意，算法使用的数值是 G' 列中列出的数值，而 G' 列中的数值又是在乘以 k 因子后得到的。

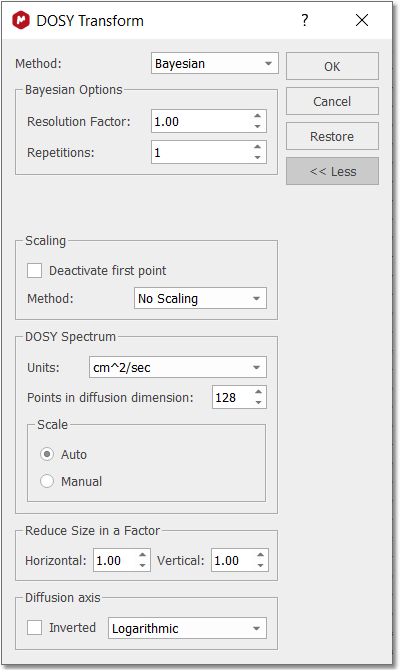
4. 运行 DOSY 变换： 只需按照菜单 "Stacked/DOSY/ROSY Transform（堆叠/DOSY/ROSY 变换）"操作即可。

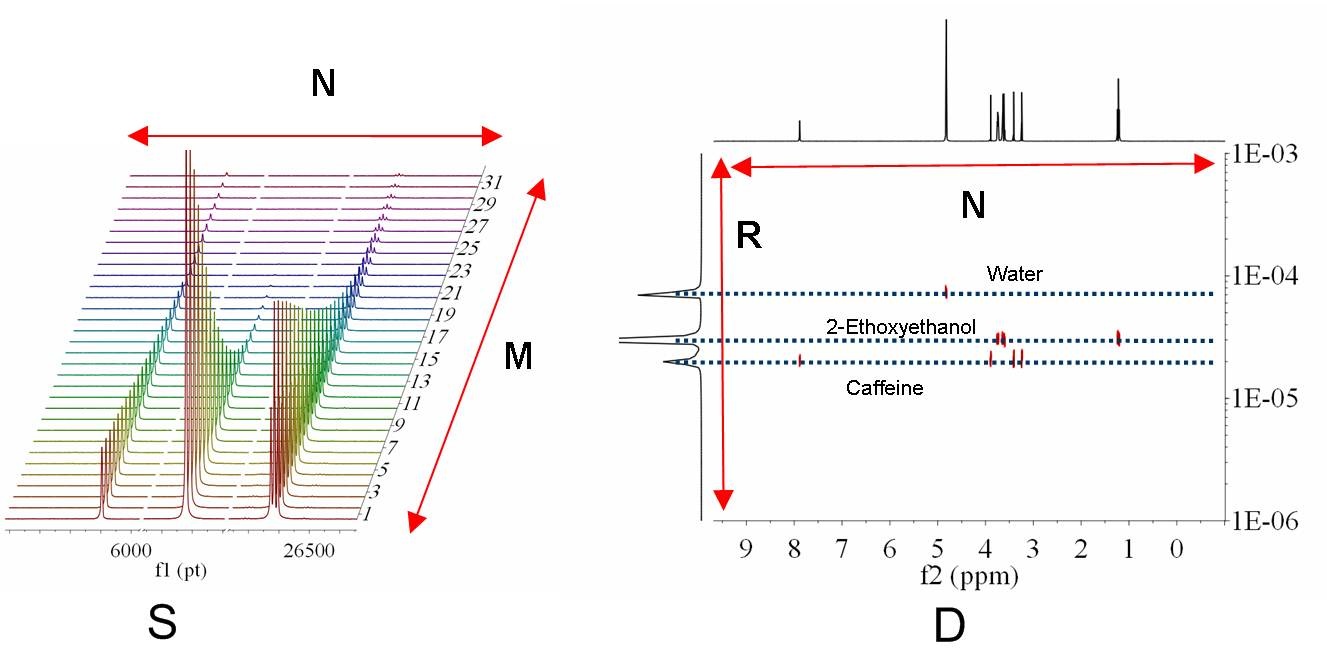
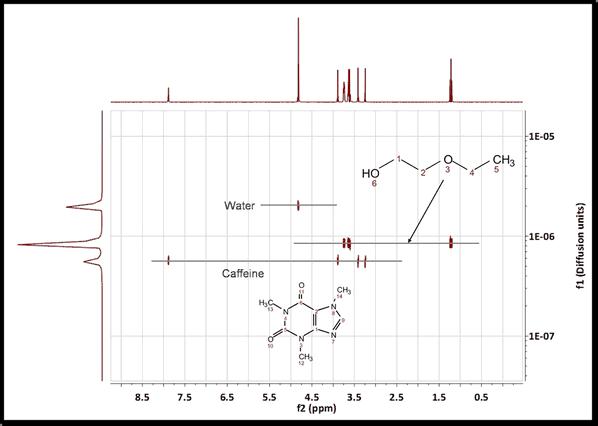
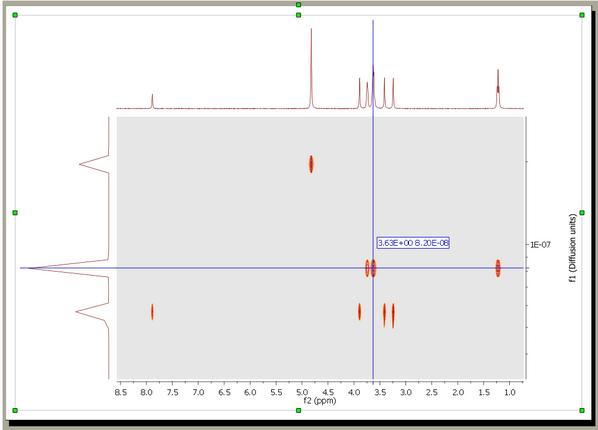
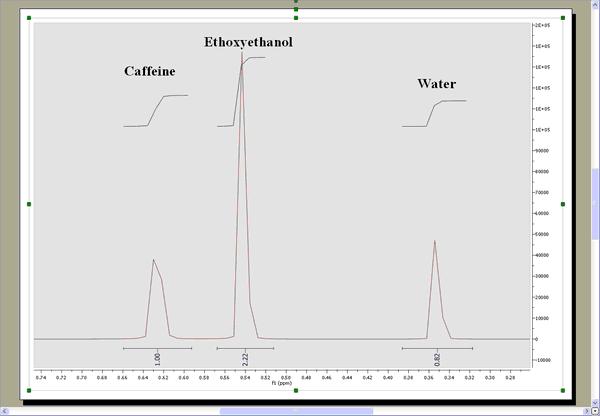
a) 首先，使用分辨率系数 1（或 0.1）。数值越大，沿扩散维度（垂直方向）的分辨率越高。但是，如果分辨率系数过高，可能会漏掉一些小峰值。

b) 初次尝试时，重复次数应保持为 0。接下来，如果想进一步提高垂直分辨率，可将该值设为 1 或 2。这样可以大幅提高分辨率，但可能会出现一些伪影。

c) 缩放：可以使用 "不缩放"、"连续缩放 "或 "缩放一半"。

连续缩放：通常用于变化大三角洲的实验，可最大限度地减少 T1 松弛对数据的影响。

缩放一半：结果中只显示堆栈中波谱集的前半部分。

如果您想放弃堆叠图中的第一个频谱，请选中 "停用第一个点 "复选框，确保最后的迹线数目为奇数。

d) 如果以 G/cm 为单位引入梯度强度，则得到的扩散系数将以 cm^2/s 为单位。

这就是得到的结果。可以看到，3 种化合物（水、乙氧基乙醇和咖啡因）完全分离。

您可以使用 "十字光标"来测量 Difussion 值。

可在3D 查看器中显示结果：

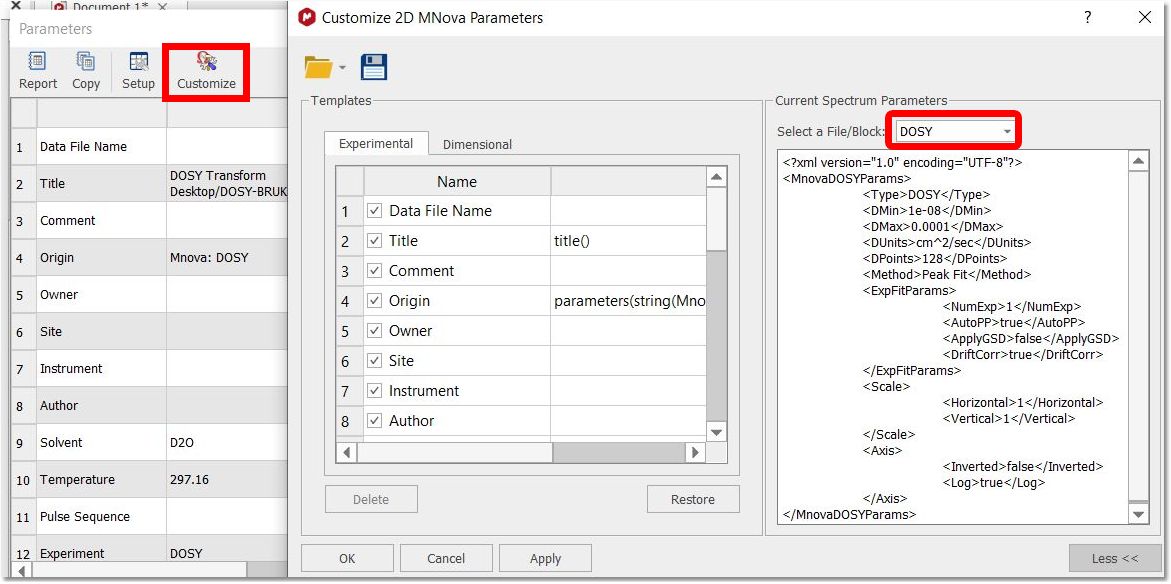
通过菜单 "View/Parameters/Customize（视图/参数/自定义）"并从下拉菜单中选择 DOSY 块，可以检查 DOSY 变换所使用的设置：

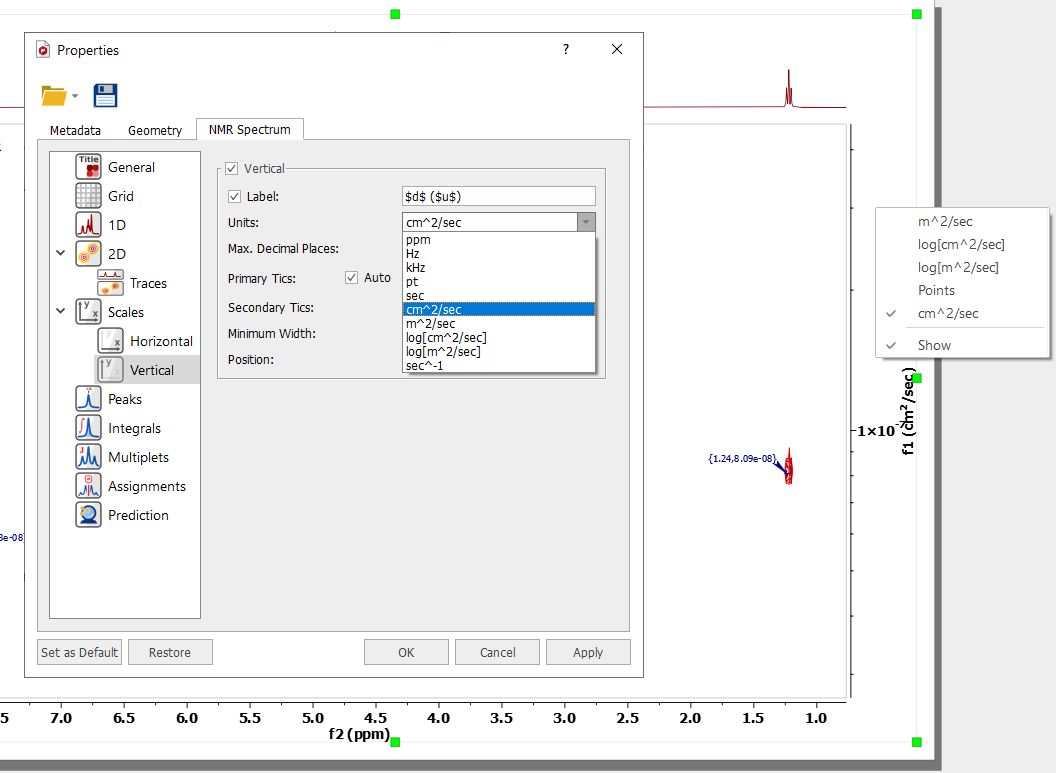
可以在 "属性 "对话框中更改扩散单位（或右键单击伪 2D 图的扩散标度）：

在贝叶斯 DOSY 变换对话框中选中 "校正非均匀梯度 "选项，即可应用非均匀梯度（NUG）校正（选项仅在数据集需要时才会出现）：

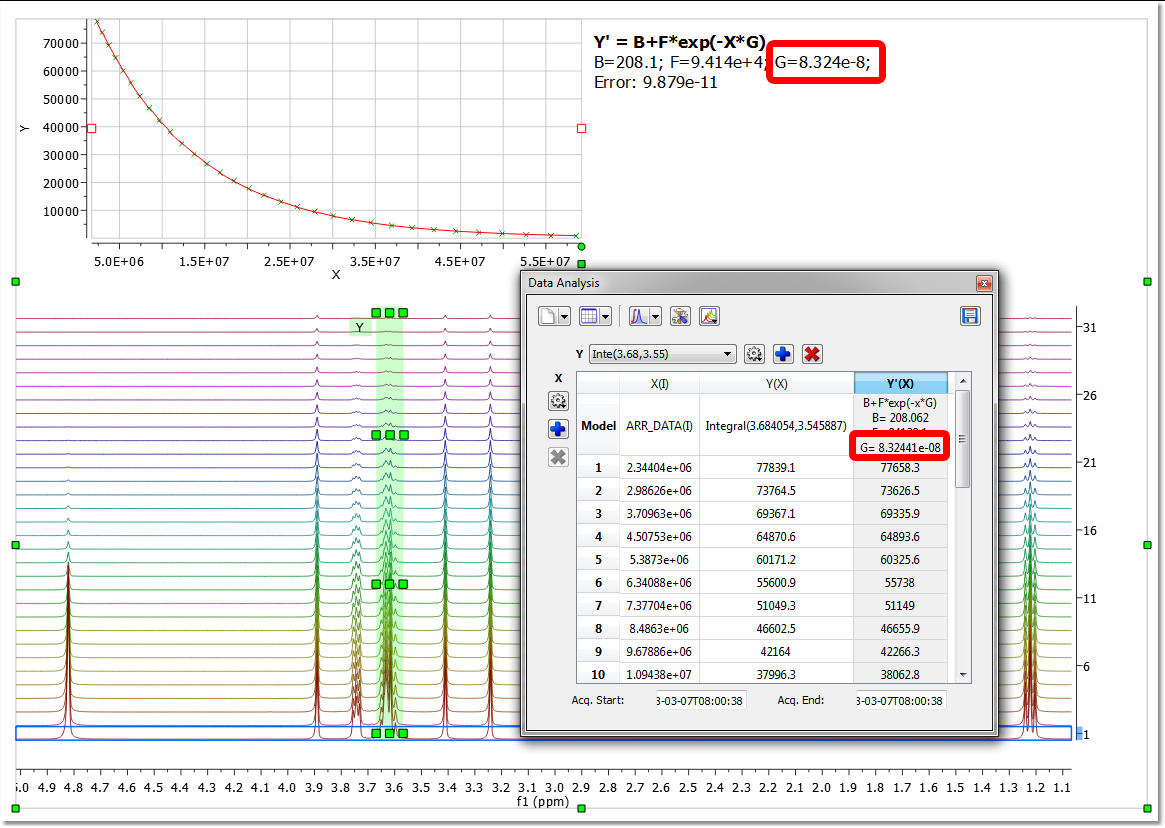
您也可以使用 "数据分析 "功能 以传统方式（由参数 G 的值给出）获取扩散系数 ：

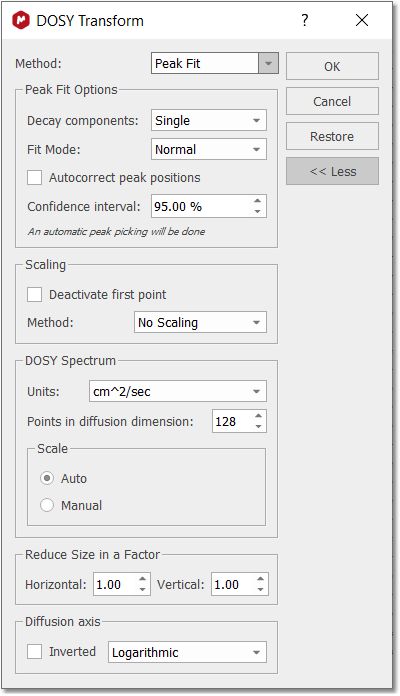
点击 "高级 "按钮后，只需选中相应选项，即可以对数标度显示扩散轴（即使垂直标度倒置）。

峰高拟合方法

在 DOSY 处理功能中增加了 "峰高拟合 "方法。现有的贝叶斯 DOSY 程序可提供系统中发现的扩散系数的完整连续图。为了提供更加 "过滤 "的 DOSY 2D 输出，并提高与其他波谱仪软件的一致性，采用了一种新的 DOSY 处理技术。

数据准备后，峰值拟合方法使用指数衰减法拟合提取的峰值强度值。如果检测到瓦里安非均匀梯度（NUG）校准，则使用校准后的 NUG 衰减代替指数衰减。最初只使用单指数、双参数（I0和R）指数衰减，这为大多数 DOSY 实验提供了高质量的结果。新功能 衰变组件自动 "允许应用多指数（最多 3 个指数成分）：

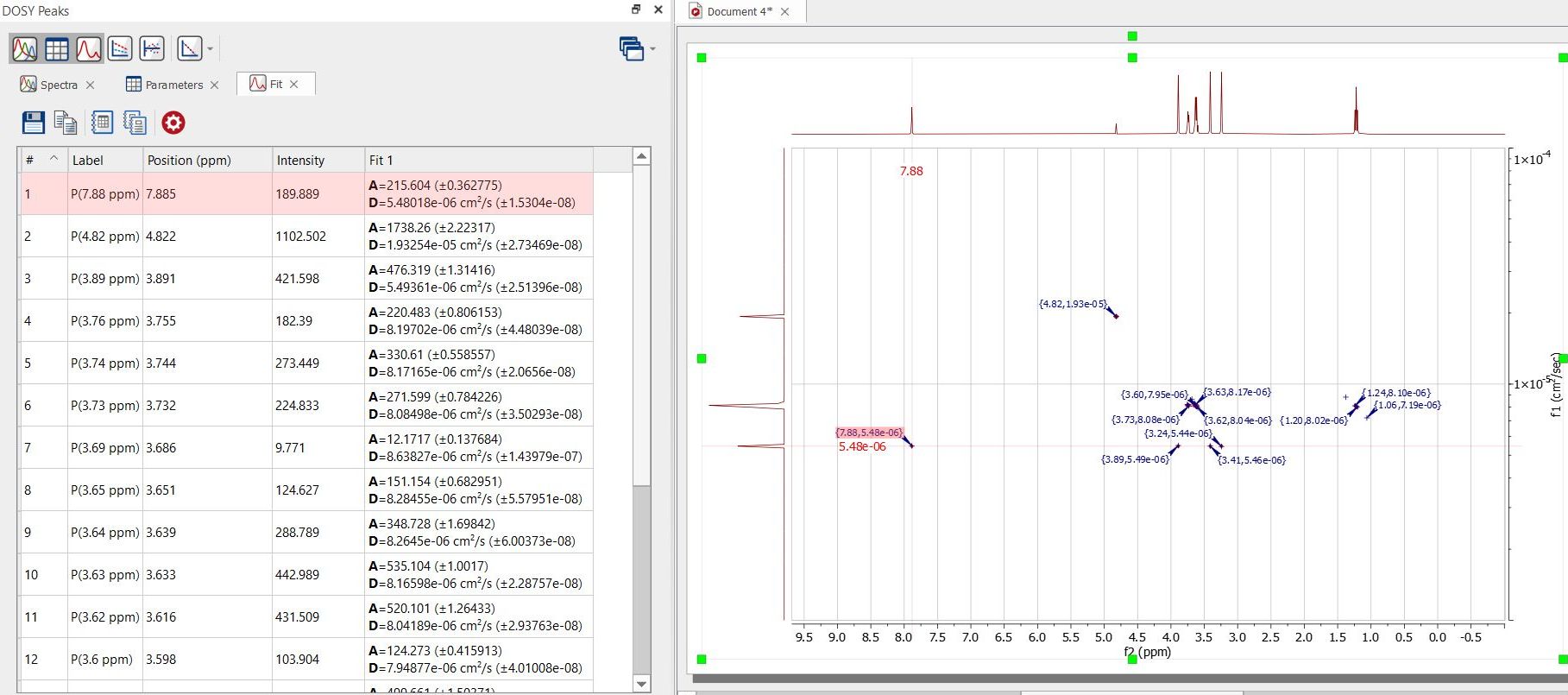
自动确定分量的数量：

-首先，使用单指数函数拟合衰变峰强度。

-分析优化方案的残差。如果残差明显超过实验噪音水平，则认为拟合效果不理想。在这种情况下，在拟合模型中添加另一个指数成分，并再次优化拟合。

-循环往复，直到达到最大分量数（最多 3 个）或获得满意的残差。

要在 DOSY/ROSY 变换对话框中选择自动多指数拟合，请选择方法（Method：Peak Fit（峰值拟合）和Decay components（衰减成分）选项：Auto（自动）。选项Decay components：单衰减分量 "选项执行旧的单指数衰减分析。单指数分析和自动多指数分析都支持 DOSY 的 NUG 校准衰变函数。

拟合模式

"加权拟合"：利用频谱中的噪声为拟合中的每个点设定误差。

"蒙特卡洛"：使用蒙特卡洛模拟估计拟合误差，将波谱误差作为标准偏差。

选项：

如果在程序启动时存在用户定义的峰值，则可以使用这些峰值来代替应用新的峰值拾取。

GSD 分析： 如果要应用 GSD 分析，则需要在应用 DOSY 变换前应用 GSD 取峰。这将对原始堆栈中的每个波谱应用 GSD，并使用 GSD 峰面积和校正小峰位置漂移来单独估算所有峰的扩散系数。对于非常复杂的波谱，该选项可能会比较慢。 如果应用GSD 分析，则会使用去卷积峰面积而不是默认峰高（标准 Mnova 峰强度）。这将有助于峰宽沿 DOSY/ROSY 实验阵列变化的情况，而且峰面积能更好地反映峰强度。使用GSD 分析时，峰漂移校正是自动进行的，因此在这种情况下不需要自动校正峰位 。

自动校正峰位： 在阵列式 DOSY 实验中，各行之间的峰位可能会略有不同。可以通过调整峰位来补偿这种影响。

该程序支持 NUG 校正。对于没有 NUG 系数的数据，将使用高效的指数拟合程序。如果存在 NUG 校正，则本程序中发现的 D 值将用作使用 NUG 校正衰变模型进行 Levenberg-Marquardt 非线性拟合的起点。

运行分析后，您将在波谱浏览器中看到伪 2D 图，并显示 "DOSY 峰 "面板：

从该面板中，您可以获取每个峰的信息以及拟合分析的扩散值。

点击 "Spectra（波谱）"按钮将显示叠加图中每个迹线的信息：

选择 "参数 "按钮将显示元数据中的一些有用信息：

选择 "拟合 "按钮将显示一个表格，其中包含每个峰的拟合值信息：

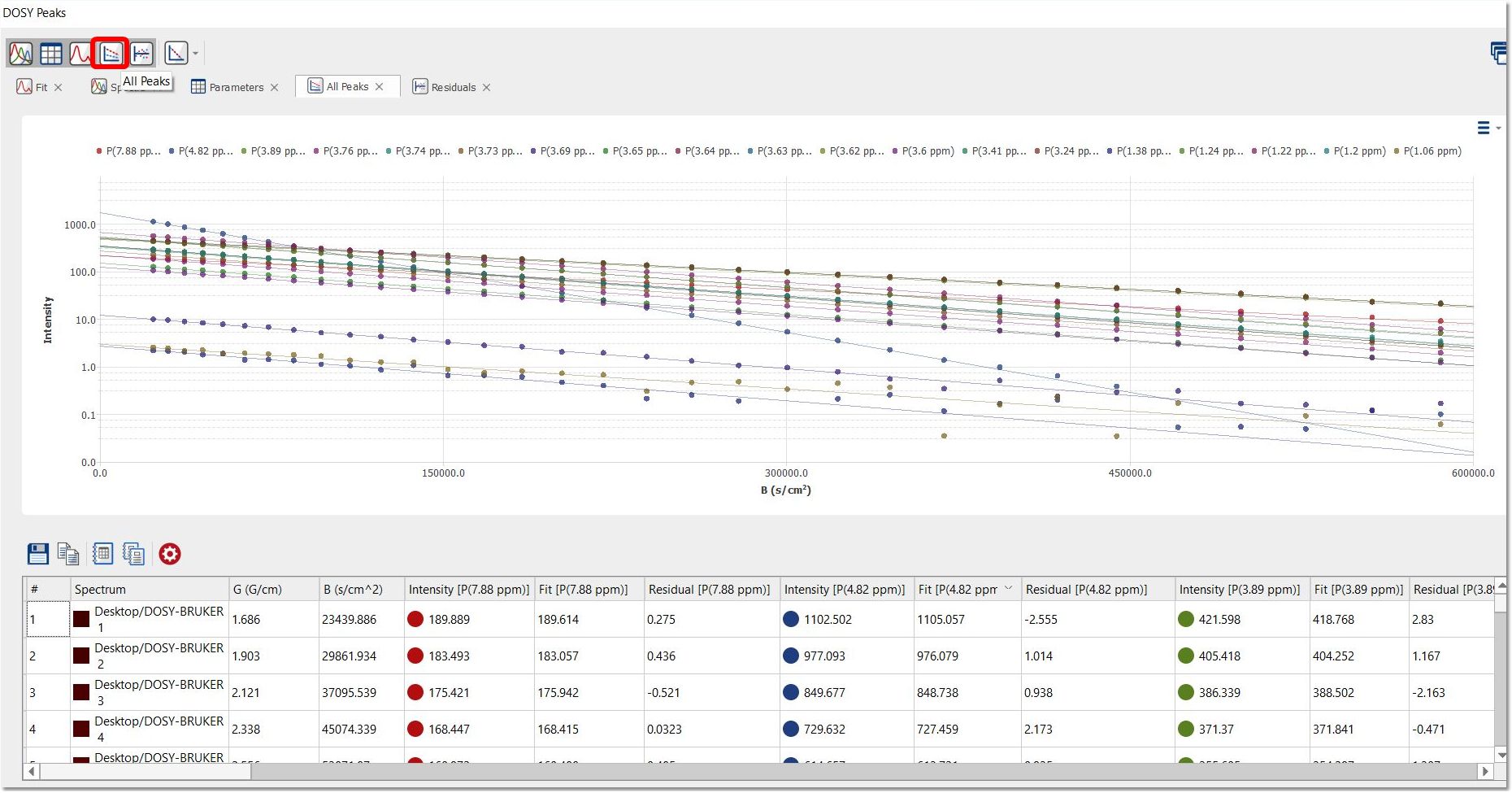
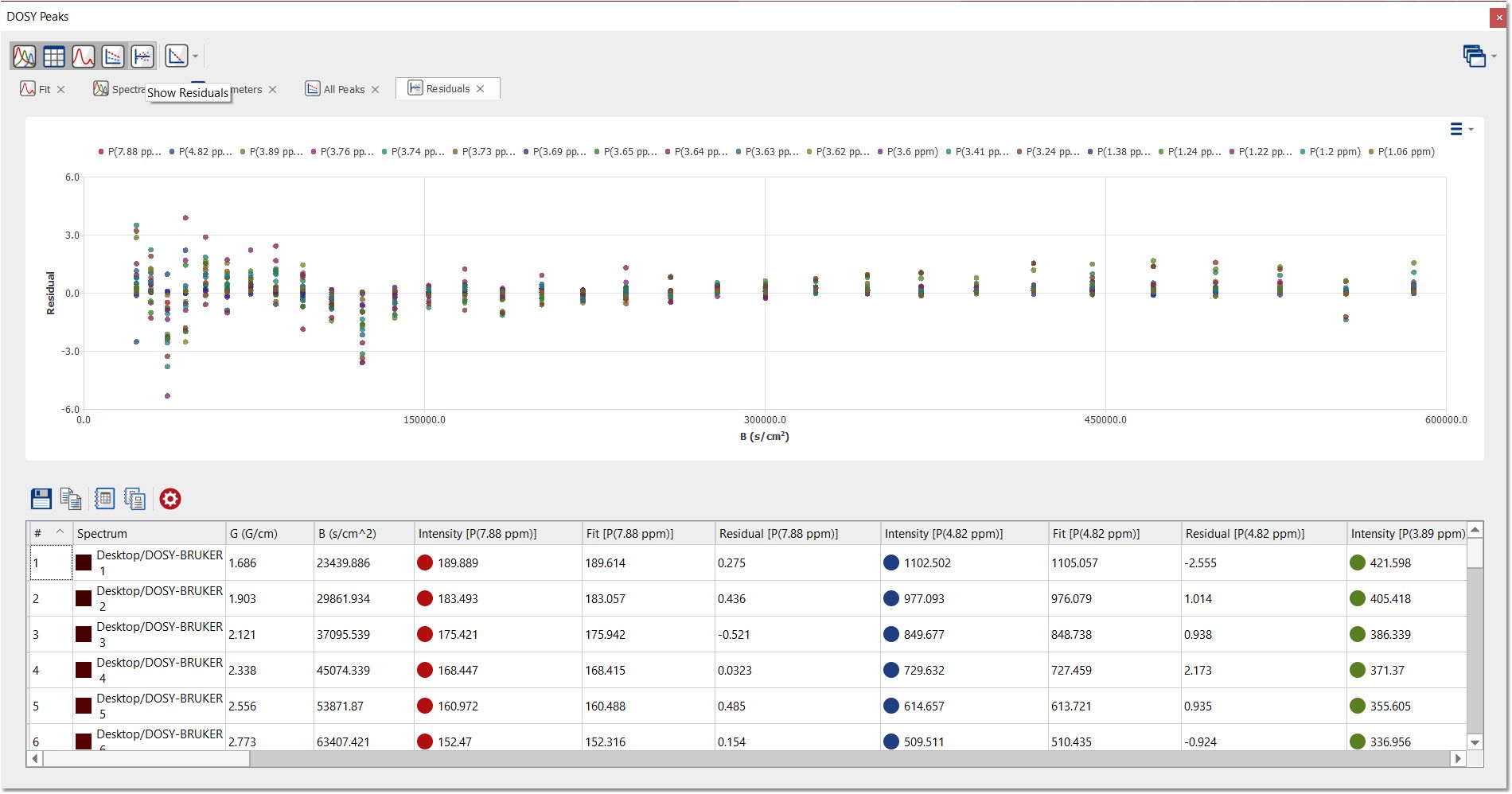
点击 "所有峰值 "按钮，显示堆叠图中适用迹线的每个峰值的强度/B 图：

点击 "显示残差 "按钮，显示每个拟合的残差：

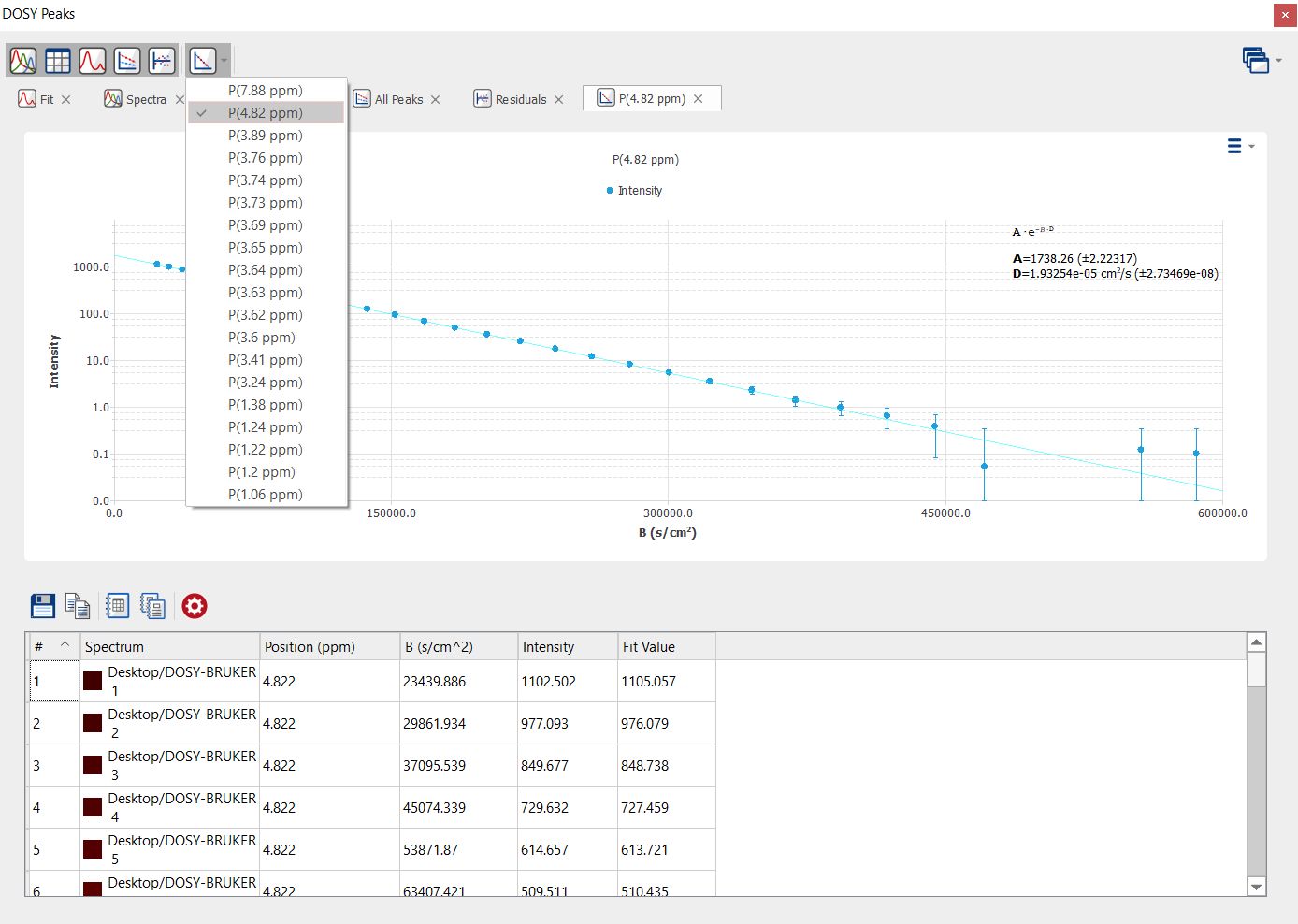
您还可以从下拉菜单中选择每个峰的单独拟合曲线：

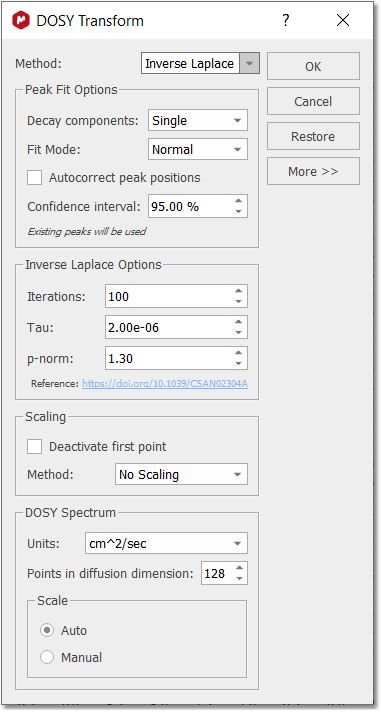
反拉普拉斯方法

反拉普拉斯变换是一种可以给出扩散系数/松弛率连续分布的技术。它是峰值拟合（Peak Fit）的替代技术，峰值拟合使用的是衰变中离散分量的数量。从受实验噪声影响的离散点数据中寻找衰变常数的分布是一个定义不清的数学问题，可能有多种解法，在数学上有效，但在化学本质上不一定有意义。为了解决这个问题，人们做了很多努力：通常使用某种正则化来限制分布搜索。例如，假设分布是 "平滑的"，具有最小的 "熵 "等。

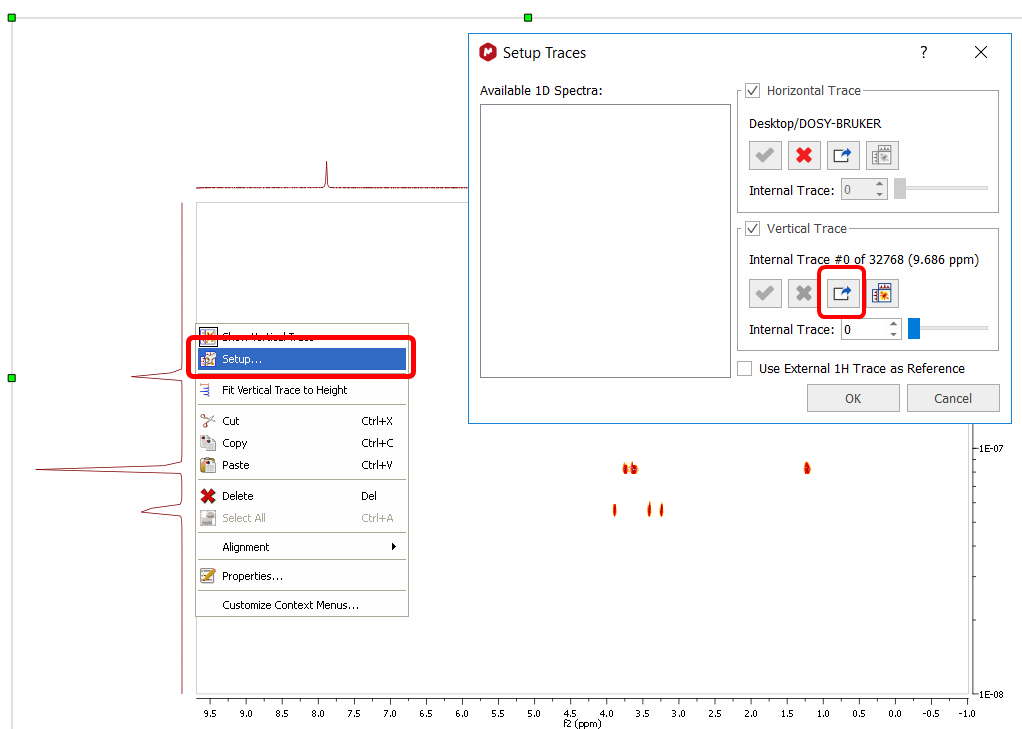
有许多选项会影响方法的性能和最终结果。如果选择了Method.Inverse_Laplace 方法，用户可以对这些选项进行修改：选择 "反拉普拉斯 "时，用户可以对这些选项进行修改。

-迭代次数：用于迭代重权最小二乘法的迭代步数。迭代步数应足够大，以便求解收敛。默认值为 100，但 20 左右的数值应能得到质量合理的解。计算时间与该参数大致成正比。

-Tau：均方根偏差与目标函数中用于优化的正则化项之间的比率。tau值越小，均方根偏差越大，但正则化的缺失会导致解的不稳定性以及解中出现许多不自然的尖峰。非常大的值会导致解的 "过度平滑化"。有关tau如何影响结果的示例，请参见原始论文和补充材料。

-P-norm：lp-norm正则化的系数 p。数值范围为 1≤p≤2。p>1 的值会产生 "平滑 "解。关于lp-norm正则化的讨论，请参见原论文。原论文提出了一种自动确定p值的方法。然而，该方法耗时过长，不适用于化学位移维度上多点的二维地图转换。因此，参数p可由用户自行调整。

在支持的平台上使用并行 CPU 计算。

扩散或弛豫尺度可以用对数或线性表示。刻度值的方向（升序或降序）也可以改变。这些更改是为了与外部 NMR 软件（如 Bruker TopSpin）兼容，同时也是为了满足一些用户的偏好。这些功能可在DOSY/ROSY 变换对话框的 "更多"部分找到。

更多信息请访问：https://doi.org/10.1039/C5AN02304A

贝叶斯 DOSY 和量化

Mnova 中的贝叶斯 DOSY 数据变换算法 (BDT) 本身是线性的，因此 "响应 "的振幅与 "输入 "成正比。然而，这并不是全部：贝叶斯方法总是涉及最终的归一化，而归一化在很大程度上是一个选择问题，在 BDT 中留下了很大的自由度。我们对生成的二维地图中的每一列进行归一化处理，使其与梯度为零的一维波谱中的点相匹配。这种列归一化看起来可能涉及一系列沿 D 轴的积分，但实际上并非如此，因为 "沿 D 尺度的积分 "没有任何意义（充其量它可以被看作是一种斯蒂尔杰斯积分，具有适当定义的 D 尺度区间权重）。这是一个技巧，一个直观的小窍门，但却大大缓解了量化问题。因此，投影中峰值积分的比率非常接近于各分量之间的比率。不过，鉴于 "沿 D 或 logD 的积分 "本质上不可能成立，我们倾向于避免使用这一概念，至少目前是这样，特别是当有人在非常宽的 D 值区间内进行积分，或比较围绕非常不同的 D 值的两个积分时。从这个角度来看，考虑到我们所采用的归一化方式，峰高是一个更为严格的量--除非某个分量的峰值在 D 轴上因人为因素而错位（因此，只对极少数 D 级点进行适度积分可能是可以接受的）。

因此，BDT 可以帮助您通过对扩散迹线进行积分来获得每种化合物的关系式。为此，只需右键单击迹线并在上下文菜单中选择 "设置"，即可显示 "设置迹线 "对话框。然后点击 "蓝色箭头 "图标，提取 "垂直轨迹"。请确保该轨迹为 "内部投影"（总和）：

这将把轨迹提取到一个新页面。最后对该迹线的信号进行积分，得出化合物的适用比率：

有关 DOSY 处理的更多信息，请参阅 本网络研讨会。