Verification Results panel

在验证结果表中，信息分布在不同页面（概述、波谱质量、诊断和测试）。可根据不一致类型过滤信息：

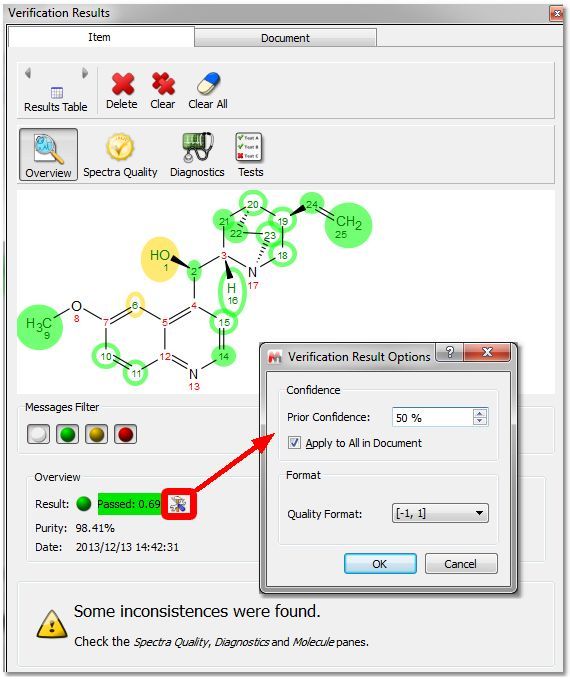
在 "概览"模式下，我们将看到结果、纯度值、日期和验证结果选项。在该对话框中，您可以将 "先验置信度 "更改为一个波谱或文档中的所有波谱（例如，如果您使用 100 个波谱运行了验证，然后想查看不同先验置信度值下的结果，而无需重新运行验证，这将非常有用），还可以更改为质量格式：

如果文档包含多个分子，您可以使用 "结果表 "箭头来浏览结果：

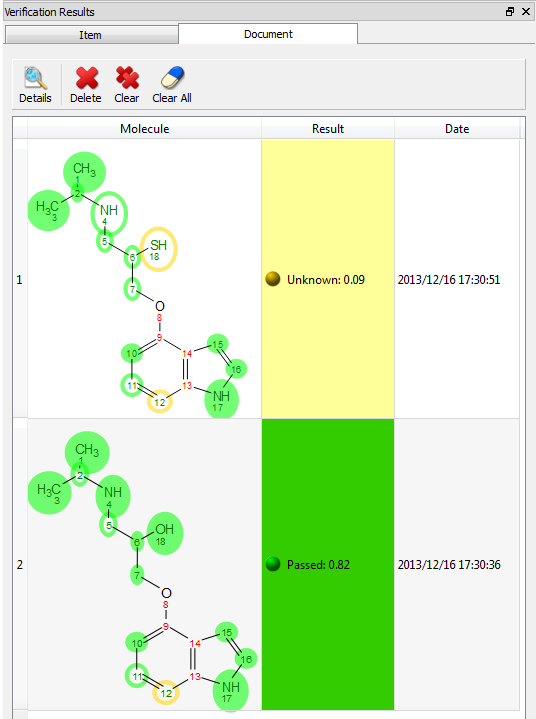
单击 "结果表 "按钮将以表格形式显示验证结果：
 

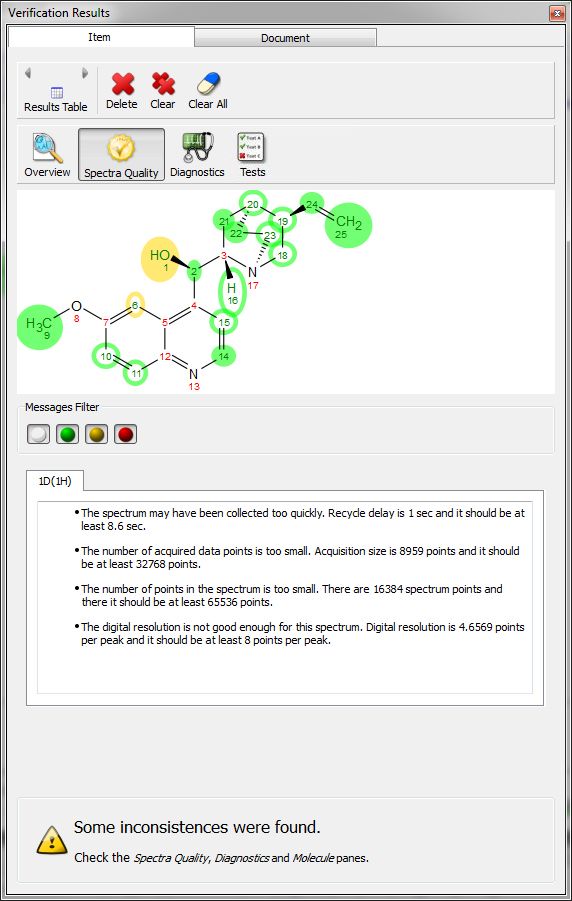
点击 "波谱质量"（Spectral Quality）按钮，将显示检测到的与实验数据质量有关的任 何问题的报告，您可以使用彩色按钮对其进行过滤：
 

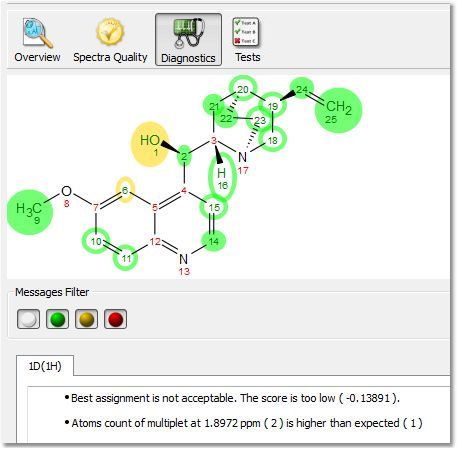
点击 "诊断 "按钮，将显示一些警告信息：

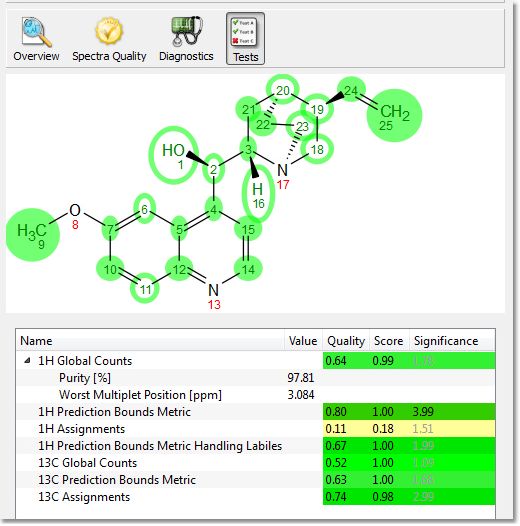
点击 "Tests（测试）"按钮，将显示每个测试的得分、重要性和质量值：

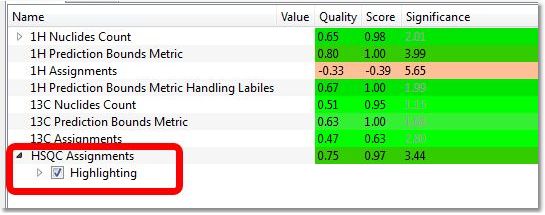
-全局计数：

纯度：这是用 NMR 计算出的样品纯度估计值。基本上，它是化合物与（杂质+人工痕迹）峰的比率。选择设置表中的 "显示纯度标签 "复选框（默认禁用），即可在峰值表中显示纯度。

最差多重影位置：这是真实多重影的位置，在化学位移标尺上与其预测的对应物相差最远。

-预测边界指标：这是在化学位移尺度上与其实验对应物相差最远的预测多重子位置。分子结构中的每个原子都有一个化学位移，并根据对其特定环境的预测质量给出一个允许 范围。然后，软件会检查在该允许范围内是否存在核素数量合适的多重元素。对于被自动编辑分析步骤标记为 Labiles 的多重化合价，将进行特定的测试。

-分配测试：缺失峰的有效数量和额外峰的有效数量（1H、13C 和 HSQC）。建立拟议分子结构的全自旋系统并与实验数据进行比较。我们列举了波谱中自旋系统（以及通过自旋系统对原子）的每一种可能的多重赋值，并通过绩优函数计算其相似性。绩优函数的最高正结果将作为验证测试结果和结构/波谱对的自动赋值进行报告。在 HSQC 中，对结构的二维波谱进行预测，每个预测峰值都有一个二维允许范围。然后对每个范围进行评估，以确定其中是否存在实际峰值，以及是否存在峰值缺失或实际峰值与允许预测范围不符的范围。

当针对多个分子运行 HSQC 验证时，用户可以通过从 ASV 结果表中选择分子并选中/取消选中表中 HSQC 分配的 "高亮显示 "框来显示每个分子的 HSQC 矩形：

-MS分子匹配得分：针对每个拟议结构的分子式和给定的电离模式（如质子化），计算分子离子簇谱。然后将每个分子离子簇谱与液相色谱或气相色谱质谱运行中的每个谱图进行比较，并根据谱图相似度进行排序，其中 1.0 表示分子离子簇 m/z 区域内的谱图完全相同。考虑到分子离子色谱（或化学色谱）的响应，这一排序将进一步细化，其最大值也为 1.0。 最终的匹配得分是两个指标的乘积。质谱分子匹配相似度测量由传统的点积计算得出，并考虑了用户指定的 m/z 精确度，以充分利用精确测量的质谱数据。如果数据集中也有 MS/MS 图谱，则会使用这些结构来预测碎片图谱，并将这些预测的碎片图谱与获取的 MS/MS 图谱进行比较。

一旦数据处理完毕并准备好进行验证，就会对所提出的结构是样品主要成分的假设进行一系列测试。对于一个有效的自动结构验证系统来说，当其考虑的许多参数（整合、波谱分析、预测化学位移等）都很可能不完美时，系统必须具备以不同方式权衡不同结果以及在特定条件下自动评估特定测试重要性的能力。这样，系统就能在输入质量不确定的情况下保持稳健。因此，单项测试可能不仅有分数，而且有不同的重要性，此外，还可能与主要结果相关。每个测试都会产生一个[质量、分数、重要性]结果：

-质量：质量：每个单项测试的质量得分是由该测试的得分和意义值组合而成的。质量得分的目的是生成一个单一的数字，以便在处理大量数据时进行比较。点击 "选项 "按钮后，可从 "验证结果表 "中选择质量值的格式：

-分数：1 表示假设与实验数据完全吻合，-1 表示假设完全失败，因此肯定是错误的。分值包括三位数字（考虑先验置信度的分值、验证分值（不考虑先验置信度）和 "先验置信度"）。

-意义：根据数据特征、拟议的分子结构、给定 HOSE 代码的预测质量或分子上存在的化学环境等，每次测试都有一个重要程度。因此，波谱中杂质含量高可能会降低严重依赖积分的测试的重要 性，而化学环境预测不准确可能会降低严重依赖化学位移预测的测试的重要性。0-2 为低显著性，3-5 为中等显著性，大于 5 为高显著性。理论上，显著性的数值没有限制，如果能设计出一种完全确定、完全无误的测试，那么在这一概念中，其显著性将是无限的。