Spin Simulation

注意：必须安装 NMRpredict Desktop 插件（无需该插件的许可证）。

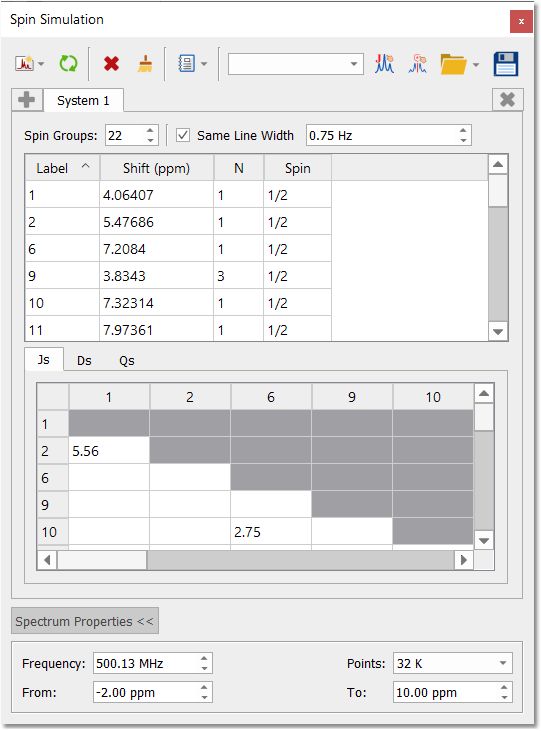
MestReNova 的这一模块是用于高分辨率 NMR 图谱的高效模拟器，可通过菜单 "View/Tables/Spin Simulation（或 Prediction/Spin Simulation）"使用，该菜单将显示适用的对话框：

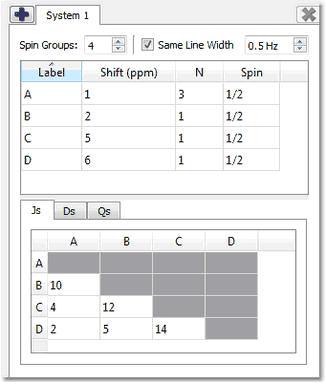
在该对话框中，我们可以通过输入所需的值轻松模拟波谱。例如，3 个质子（3 个自旋组）分别称为 A、B 和 C，化学位移分别为 1、5 和 7 ppm。它们的耦合常数分别为 J(AB) = 3Hz、J(BC) = 5.5Hz 和 J(CA) = 3.4Hz。最后，选择点数和波谱限制，点击 "新建模拟 "按钮生成相应的波谱：

模拟出频谱后，您可以修改表中的任何值，并点击 "重新计算 "按钮获得新频谱 .点击 "删除 "按钮可从表格中删除特定行，或点击 "全部清除 "按钮从头开始。您可以引入 "二极性 "或 "四极性 "耦合常数，并通过点击相应方框并输入所需数值来更改 "核数目"、"自旋 "和 "线宽 "值。最后，点击 "重新计算 "按钮更新波谱中的变化。

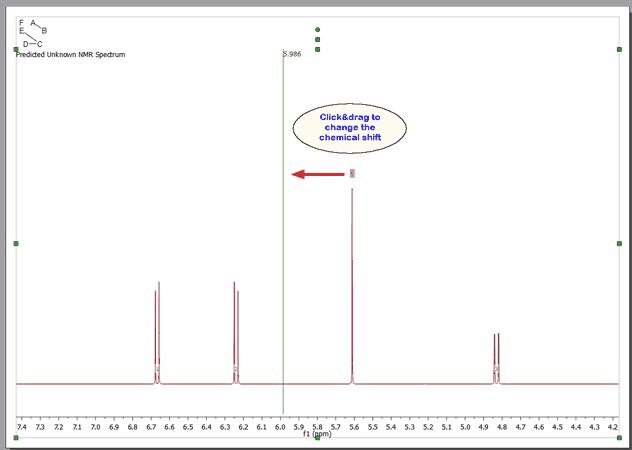
点击并拖动赋值标签可更改自旋模拟波谱中任何信号的化学位移：

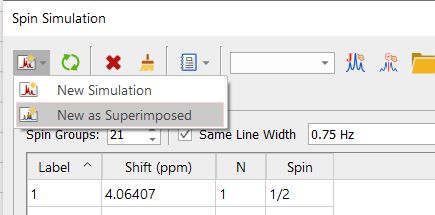
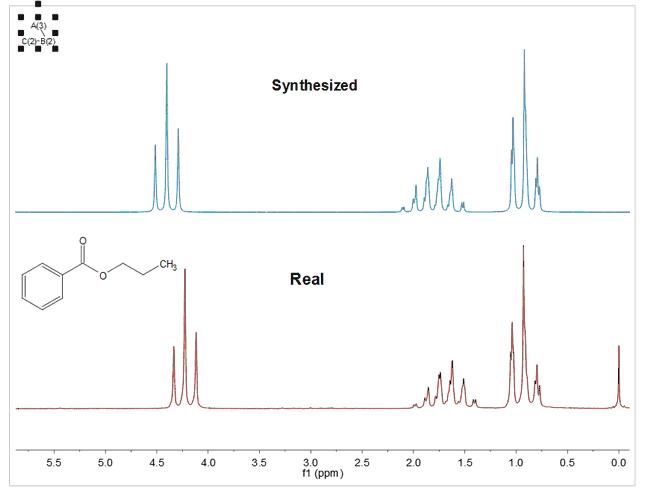
在实验波谱上选择 "新建为叠加"，将合成波谱与实验波谱叠加在一起：

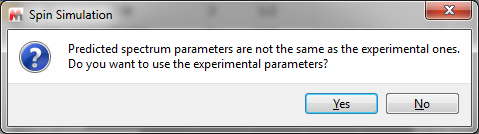
如果实验波谱和模拟波谱的参数不一致，当您尝试以叠加方式生成计算波谱时，将显示一条 信息：

点击 "是"，将修改波谱属性参数，使其与实验参数一致。

下面是另一个实验数据集与模拟数据集的比较示例：
 

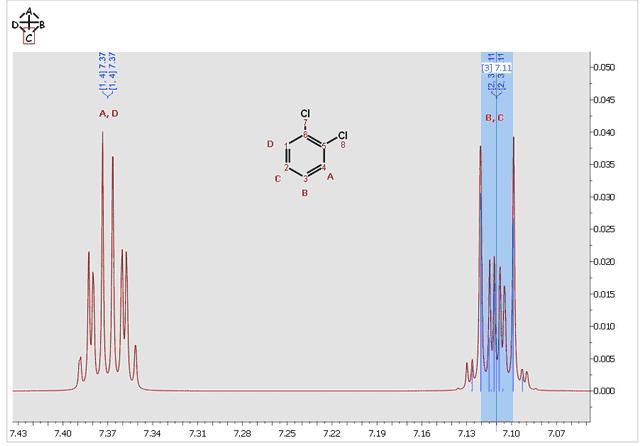
您可以在下面看到 "orto-dichlorobencene "的模拟波谱；这是一个 AA'BB' 系统：

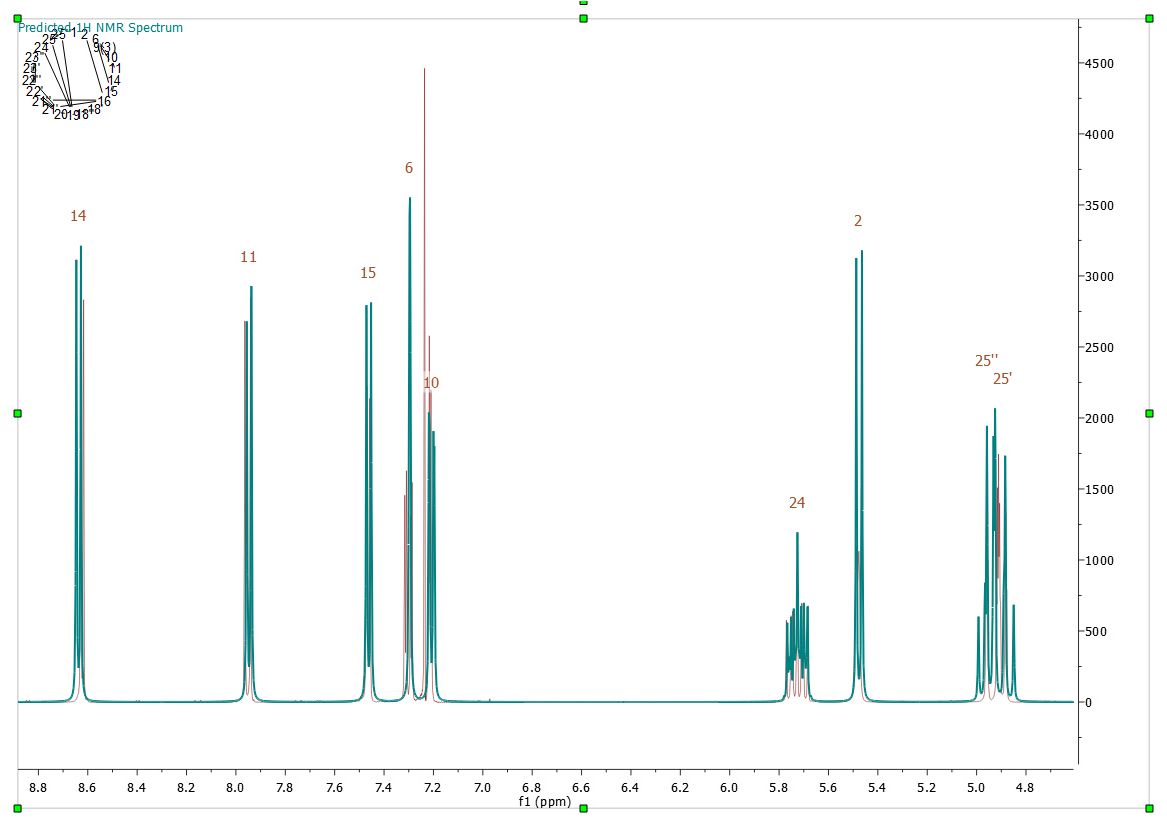
如何模拟 A3BXY 系统？

下面是一个 A3BXY 系统的示例：

要得到上表，只需按照以下步骤操作：

1.首先，创建一个有 4 个自旋组的系统。请注意，A3 是一个具有 3 个等效磁自旋的唯一自旋群，因此需要在标签 A 中输入 N=3。

2.2. 然后，输入其他原子核（B、C、D）的所需值，所有原子核的 N=1 （同时输入所需的化学位移值）。请注意，Mnova 不需要知道耦合是强还是弱，因为 Mnova 是通过考虑化学位移和耦合常数的严格方法进行量子计算的 3.

3.输入所有数值并选择拉莫尔频率和数字点数量、每个原子核的线宽等之后，只需点击 "新建模拟 "按钮即可得到合成波谱。

如何添加新系统？

点击 "添加系统 "按钮 来添加多个系统。新系统将是分子的一个片段，由于其质子不与其他质子相互作用，因此可以单独模拟。换句话说，就是一组通过耦合常数相互关联的原子核。添加新系统后，您可以使用 "种群 "编辑框更改系统的种群。

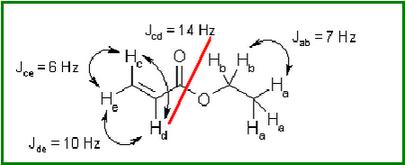
以丙烯酸乙酯 CH2CHCOOC2H5 这种小分子为例

如您所见，对该分子的 1H-NMR 波谱进行标准模拟需要引入八个频率，每个质子一个。此外，还需要引入九个耦合常数。不过，即使是对这个自旋系统的简单研究，也能为我们提供一个更优雅的解决方案。

为什么不把这个自旋系统看作两个 "子系统 "呢？一个 "子系统 "与乙基相对应，由五个质子组成，只有两个不同的频率，分别为 a（甲基）和 b（亚甲基），只有一个耦合常数 Jab。另一个 "子系统 "由剩余的三个质子（乙烯基的质子）组成，有三个频率（c、d 和 e）和三个耦合常数（Jcd、Jce 和 Jde）。将自旋系统分解为两个子系统是可能的，因为它们之间没有任何联系。自旋系统分解成子系统的过程可以在许多分子中进行，例如，这就是核磁共振波谱数据表的概念基础。

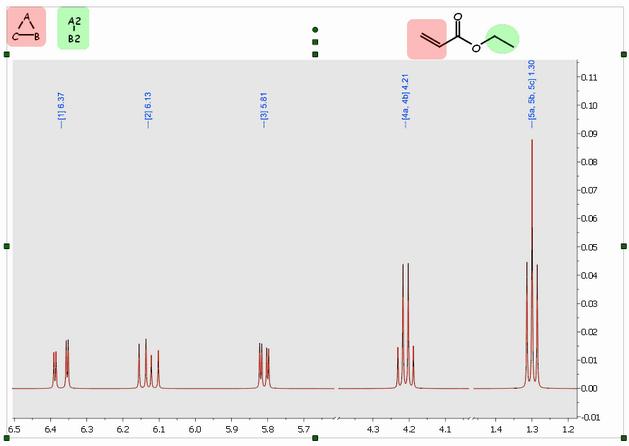
下面是丙烯酸乙酯的合成波谱；在创建了两个不同的系统后，系统 A（乙烯基质子）为红色，系统 B（乙基）为绿色：

这种分解方法大大提高了计算速度，因为计算的复杂性会随着所考虑的自旋（原子核）数量的增加而呈指数增长。不过，我们还可以进一步提高计算速度和灵活性。

为什么不只引入五个频率，并告诉程序每个频率对应多少个质子呢？引入磁性等价后，就可以使用从 a 到 e 的五个自旋组及其相应频率进行计算。前两个自旋组 a 和 b 分别有三个和两个质子，而其他三个自旋组则各有一个质子。当然，我们只需要四个耦合常数：Jab、Jcd、Jce 和 Jde。这个过程可以在许多分子中进行。